
【题目】如图1,已知直线l:y=﹣x+2与y轴交于点A,抛物线y=(x﹣1)2+k经过点A,其顶点为B,另一抛物线y=(x﹣h)2+2﹣h(h>1)的顶点为D,两抛物线相交于点C.
(1)求点B的坐标,并说明点D在直线l上的理由;
(2)设交点C的横坐标为m.
交点C的纵坐标可以表示为:或;
(3)如图2,若∠ACD=90°,求m的值.
【答案】
(1)
解:当x=0时候,y=﹣x+2=2,
∴A(0,2),
把A(0,2)代入y=(x﹣1)2+k,得1+k=2
∴k=1,
∴y=(x﹣1)2+1,
∴B(1,1)
∵D(h,2﹣h)
∴当x=h时,y=﹣x+2=﹣h+2=2﹣h
∴点D在直线l上
(2)(m﹣1)2+1;(m﹣h)2﹣h+2
(3)解:过点C作y轴的垂线,垂足为E,过点D作DF⊥CE于点F
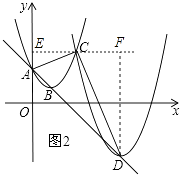
∵∠ACD=90°,
∴∠ACE=∠CDF
又∵∠AEC=∠DFC
∴△ACE∽△CDF
∴ ![]()
又∵C(m,m2﹣2m+2),D(2m,2﹣2m),
∴AE=m2﹣2m,DF=m2,CE=CF=m
∴ ![]() =
= ![]()
∴m2﹣2m=1
解得:m=± ![]() +1
+1
∵h>1
∴m= ![]() >
> ![]()
∴m= ![]() +1
+1
【解析】解: (2)(m﹣1)2+1或(m﹣h)2﹣h+2
由题意得(m﹣1)2+1=(m﹣h)2﹣h+2,
整理得2mh﹣2m=h2﹣h
∵h>1
∴m= ![]() =
= ![]() .
.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,已知y= ![]() (x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q连接AQ,取AQ的中点为C.
(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q连接AQ,取AQ的中点为C.
(1)如图2,连接BP,求△PAB的面积;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为2 ![]() ,求此时P点的坐标;
,求此时P点的坐标;
(3)当点Q在射线BD上时,且a=3,b=1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,8),点P在边BC上以每秒1个单位长的速度由点C向点B运动,同时点Q在边AB上以每秒a个单位长的速度由点A向点B运动,运动时间为t秒(t>0).
(1)若反比例函数y= ![]() 图象经过P点、Q点,求a的值;
图象经过P点、Q点,求a的值;
(2)若OQ垂直平分AP,求a的值;
(3)当Q点运动到AB中点时,是否存在a使△OPQ为直角三角形?若存在,求出a的值,若不存在请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位同学在操场上互相传球,假设他们相互间传球是等可能的,并且由甲首先开始传球.
(1)经过2次传球后,球仍回到甲手中的概率是;
(2)请用列举法(画树状图或列表)求经过3次传球后,球仍回到甲手中的概率;
(3)猜想并直接写出结论:经过n次传球后,球传到甲、乙这两位同学手中的概率:P(球传到甲手中)和P(球传到乙手中)的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个矩形的一边是另一边的两倍,则称这个矩形为方形,如图1,矩形ABCD中,BC=2AB,则称ABCD为方形.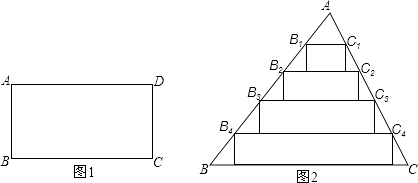
(1)设a,b是方形的一组邻边长,写出a,b的值(一组即可).
(2)在△ABC中,将AB,AC分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使这些矩形的边B1C1 , B2C2 , B3C3 , B4C4的对边分别在B2C2 , B3C3 , B4C4 , BC上,如图2所示.
①若BC=25,BC边上的高为20,判断以B1C1为一边的矩形是不是方形?为什么?
②若以B3C3为一边的矩形为方形,求BC与BC边上的高之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( ) 
A.abc<0
B.2a+b<0
C.a﹣b+c<0
D.4ac﹣b2<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com