
已知关于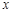 的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a、b、c分别为△ABC三边的长.
的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
(1)△ABC是等腰三角形;理由见解析;(2)△ABC是直角三角形;理由见解析; (3)x1=0,x2=-1.
【解析】
试题分析:(1)直接将x=-1代入得出关于a,b的等式,进而得出a=b,即可判断△ABC的形状;
(2)利用根的判别式进而得出关于a,b,c的等式,进而判断△ABC的形状;
(3)利用△ABC是等边三角形,则a=b=c,进而代入方程求出即可.
试题解析:(1)△ABC是等腰三角形;
理由:∵x=-1是方程的根,
∴(a+c)×(-1)2-2b+(a-c)=0,
∴a+c-2b+a-c=0,
∴a-b=0,
∴a=b,
∴△ABC是等腰三角形;
(2)∵方程有两个相等的实数根,
∴(2b)2-4(a+c)(a-c)=0,
∴4b2-4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形;
(3)当△ABC是等边三角形,
∴(a+c)x2+2bx+(a-c)=0,可整理为:
2ax2+2ax=0,
∴x2+x=0,
解得:x1=0,x2=-1.
考点:一元二次方程的应用.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源:2014-2015学年山东省泰安市毕业生学业水平模拟二数学试卷(解析版) 题型:解答题
如图,在△ABC中,∠C=90°,AC+BC=9,点O是斜边AB上一点,以O为圆心2为半径的圆分别与AC、BC相切于点D、E。
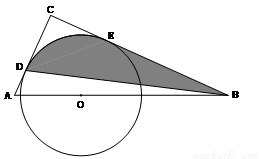
(1)求AC、BC的长;
(2)若AC=3,连接BD,求图中阴影部分的面积(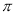 取3.14)。
取3.14)。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省泰安市毕业生学业水平模拟二数学试卷(解析版) 题型:选择题
如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积是
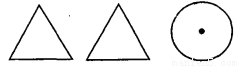
A. B.
B. 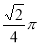 C.
C. 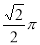 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古化德县第三中学九年级上学期期末测试数学试卷(解析版) 题型:填空题
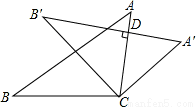
如图,将△ABC绕着点C按顺时针方向旋转40°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古化德县第三中学九年级上学期期末测试数学试卷(解析版) 题型:选择题
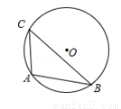
如图,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为( )
A.1 B.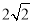 C.2 D.
C.2 D.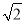
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com