
【题目】如图,在平面直角坐标系中,点A(1,0)、B(11,0),点C为线段AB上一动点,以AC为直径的⊙D的半径DE⊥AC,△CBF是以CB为斜边的等腰直角三角形,且点E、F都在第四象限,当点F到过点A、C、E三点的抛物线的顶点的距离最小时,该抛物线的解析式为 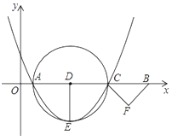
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证: 
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别,随机从箱子里取出1个球,放回搅匀再取一次,请你用画树状图或列表的方法表示所有可能出现的结果,求两次取出的都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形.请列举出所有满足条件的三角形.
(2)用直尺和圆规作出三边满足a<b<c的三角形(用给定的单位长度,不写作法,保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,端点为P的两条射线分别交两直线l1、l2于A、C、B、D四点,已知∠PBA=∠PDC,∠l=∠PCD,求证:∠2+∠3=180°.
证明:∵∠PBA=∠PDC( )
∴ (同位角相等,两直线平行)
∴∠PAB=∠PCD( )
∵∠1=∠PCD( )
∴ (等量代换)
∴PC//BF(内错角相等,两直线平行),
∴∠AFB=∠2( )
∵∠AFB+∠3=180°( )
∴∠2+∠3=180°(等量代换)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三个顶点A,B,C的坐标分别为A(4,0),B(0,-3),C(2,-4).

(1)在如图的平面直角坐标系中画出△ABC关于x轴对称的△A'B'C',并分别写出A′,B′,C′的坐标;
(2)将△ABC向左平移5个单位,请画出平移后的△A″B″C″,并写出△A″B″C″各个顶点的坐标;
(3)求出(2)中的△ABC在平移过程中所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.

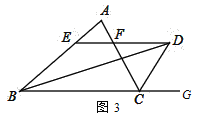
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com