
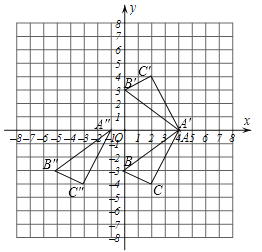
【题目】已知△ABC的三个顶点A,B,C的坐标分别为A(4,0),B(0,-3),C(2,-4).

(1)在如图的平面直角坐标系中画出△ABC关于x轴对称的△A'B'C',并分别写出A′,B′,C′的坐标;
(2)将△ABC向左平移5个单位,请画出平移后的△A″B″C″,并写出△A″B″C″各个顶点的坐标;
(3)求出(2)中的△ABC在平移过程中所扫过的面积.
【答案】(1)A′(4,0),B′(0,3),C′(2,4);(2)A″(-1,0),B″(-5,-3),C″(-3,-4);(3)25
【解析】试题分析:(1)根据网格结构找出点A、B、C以及点A′,B′,C′位置,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标;
(2)根据网格结构找出点A、B、C向左平移5个单位的对应点A″、B″、C″,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标;
(3)根据△ABC扫过的面积等于一个平行四边形的面积加上△ABC的面积列式计算即可得解.
试题解析:解:(1)△ABC如图所示,A′(4,0),B′(0,3),C′(2,4);
(2)△A″B″C″如图所示,A″(﹣1,0),B″(﹣5,﹣3),C″(﹣3,﹣4);
(3)△ABC在平移过程中所扫过的面积=5×4+(4×4﹣![]() ×4×3﹣
×4×3﹣![]() ×1×2﹣
×1×2﹣![]() ×2×4)=20+(16﹣6﹣1﹣4)=20+5=25.
×2×4)=20+(16﹣6﹣1﹣4)=20+5=25.


科目:初中数学 来源: 题型:
【题目】下列说法:
①两点确定一条直线;
②两点之间,线段最短;
③若∠AOC=![]() ∠AOB,则射线OC是∠AOB的平分线;
∠AOB,则射线OC是∠AOB的平分线;
④连接两点之间的线段叫做这两点间的距离;
⑤学校在小明家南偏东25°方向上,则小明家在学校北偏西25°方向上.
其中正确的有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(1,0)、B(11,0),点C为线段AB上一动点,以AC为直径的⊙D的半径DE⊥AC,△CBF是以CB为斜边的等腰直角三角形,且点E、F都在第四象限,当点F到过点A、C、E三点的抛物线的顶点的距离最小时,该抛物线的解析式为 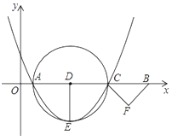
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑3 000元,购买1台学习机800元.
(1)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168 000元,则购买平板电脑最多多少台?
(2)在(1)的条件下,购买学习机的台数不超过平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.
(1)写出数轴上点A、C表示的数;
(2)点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN=![]() CQ.设运动的时间为t(t>0)秒.
CQ.设运动的时间为t(t>0)秒.
①数轴上点M、N表示的数分别是 (用含t的式子表示);
②t为何值时,M、N两点到原点的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线AB上一点,∠COE是直角,OF平分∠AOE.
(1)如图①,若∠COF=34°,则∠BOE=________;若∠COF=n°,则∠BOE=________;∠BOE与∠COF的数量关系为________________.
(2)当射线OE绕点O逆时针旋转到如图②的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
(3)在图③中,若∠COF=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半?若存在,请求出∠BOD的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.
(1)设x天后每千克该海鲜的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批海鲜一次性出售.设这批海鲜的销售总额为P元,试写出P与x之间的函数关系式;
(3)小李将这批海鲜存放多少天后出售可获得最大利润,最大利润是多少元?(利润W=销售总额﹣收购成本﹣各种费用)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com