
ЁОЬтФПЁПШчЭМЃЌ ABCD ЕФЖдНЧЯп AC ЁЂ BD ЯрНЛгкЕуO ЃЌ BD 12cm ЃЌ AC 6cm ЃЌЕу E дкЯпЖЮ BO ЩЯДгЕу B вд1cm / s ЕФЫйЖШЯђЕу O дЫЖЏЃЌЕу F дкЯпЖЮOD ЩЯДгЕуO вд 2cm / s ЕФЫйЖШЯђЕу D дЫЖЏЃЎ
ЃЈ1ЃЉШєЕу E ЁЂF ЭЌЪБдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊt УыЃЌЕБt ЮЊКЮжЕЪБЃЌЫФБпаЮ AECF ЪЧЦНааЫФБпаЮЃЎ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЕБ AB ЮЊКЮжЕЪБЃЌ AECF ЪЧСтаЮЃЛ
ЃЈ3ЃЉЧѓЃЈ2ЃЉжаСтаЮ AECF ЕФУцЛ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉtЃН2sЃЛЃЈ2ЃЉAB=![]() ЃЛЃЈ3ЃЉ24.
ЃЛЃЈ3ЃЉ24.
ЁОНтЮіЁП
ЃЈ1ЃЉШєЪЧЦНааЫФБпаЮЃЌдђга6tЃН2tЃЌМДПЩЧѓЕУtжЕЃЛ
ЃЈ2ЃЉШєЪЧСтаЮЃЌдђACДЙжБгкBDЃЌМДгаAO2ЃЋBO2ЃНAB2ЃЌЙЪABПЩЧѓЃЛ
ЃЈ3ЃЉгЩЃЈ1ЃЉЃЈ2ЃЉПЩжЊЕБtЃН2sЃЌAB=![]() ЪБЃЌЫФБпаЮAECFЪЧСтаЮЃЌЧѓЕУEFЃН8ЃЌгкЪЧЕУЕННсТлЃЎ
ЪБЃЌЫФБпаЮAECFЪЧСтаЮЃЌЧѓЕУEFЃН8ЃЌгкЪЧЕУЕННсТлЃЎ
НтЃКЃЈ1ЃЉЁпЫФБпаЮABCDЮЊЦНааЫФБпаЮЃЌ
ЁрAOЃНOCЃЌEOЃНOFЃЌ
ЁпBOЃНODЃН6cmЃЌ
ЁрEOЃН6tЃЌOFЃН2tЃЌ
Ёр6tЃН2tЃЌ
ЁрtЃН2sЃЌ
ЁрЕБtЮЊ2УыЪБЃЌЫФБпаЮAECFЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШєЫФБпаЮAECFЪЧСтаЮЃЌдђACЁЭBDЃЌ
ЁрAO2ЃЋBO2ЃНAB2ЃЌ
ЁрABЃН![]() ЃН
ЃН![]() ЃЛ
ЃЛ
ЁрЕБABЮЊ![]() ЪБЃЌAECFЪЧСтаЮЃЛ
ЪБЃЌAECFЪЧСтаЮЃЛ
ЃЈ3ЃЉгЩЃЈ1ЃЉЃЈ2ЃЉПЩжЊЕБtЃН2sЃЌAB=![]() ЪБЃЌЫФБпаЮAECFЪЧСтаЮЃЌ
ЪБЃЌЫФБпаЮAECFЪЧСтаЮЃЌ
ЁрEOЃН6t=4ЃЌ
ЁрEF=8ЃЌ
ЁрСтаЮAECFЕФУцЛ§ЃН![]() ЃЌ
ЃЌ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
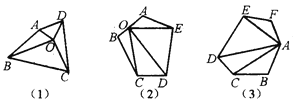
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌOЮЊЫФБпаЮABCDФквЛЕуЃЌСЌНгOAЁЂOBЁЂOCЁЂOCПЩвдЕУМИИіШ§НЧаЮЃПЫќгыБпЪ§гаКЮЙиЯЕЃП
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌOдкЮхБпаЮABCDEЕФABЩЯЃЌСЌНгOCЁЂODЁЂOEЃЌПЩвдЕУЕНМИИіШ§НЧаЮЃПЫќгыБпЪ§гаКЮЙиЯЕЃП
ЃЈ3ЃЉШчЭМЃЈ3ЃЉЃЌЙ§AзїСљБпаЮABCDEFЕФЖдНЧЯпЃЌПЩвдЕУЕНМИИіШ§НЧаЮЃПЫќгыБпЪ§гаКЮЙиЯЕЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
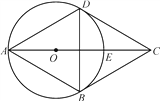
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЫФБпаЮABCDЮЊСтаЮЃЌЁїABDЕФЭтНгдВЁбOгыCDЯрЧагкЕуDЃЌНЛACгкЕуE.
(1)ХаЖЯЁбOгыBCЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєCE=2ЃЌЧѓЁбOЕФАыОЖr.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
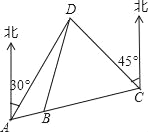
ЁОЬтФПЁПЁАБМХмАЩЃЌажЕмЃЁЁБНкФПзщдЄЩшМЦвЛИіаТгЮЯЗЃКЁАБМХмЁБТЗЯпAЁЂBЁЂCЁЂDЫФЕиЃЌШчЭМAЁЂBЁЂCШ§ЕидкЭЌвЛжБЯпЩЯЃЌDдкAББЦЋЖЋ30ЁуЗНЯђЃЌдкCББЦЋЮї45ЁуЗНЯђЃЌCдкAББЦЋЖЋ75ЁуЗНЯђЃЌЧвBD=BC=40mЃЌДгAЕиЕНDЕиЕФОрРыЪЧ_____mЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
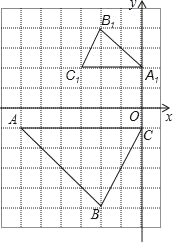
ЁОЬтФПЁПШчЭМЃЌЁїABCгыЁїA1B1C1ЪЧЮЛЫЦЭМаЮЃЎ
ЃЈ1ЃЉдкЭјИёЩЯНЈСЂЦНУцжБНЧзјБъЯЕЃЌЪЙЕУЕуAЕФзјБъЮЊЃЈЉ6ЃЌЉ1ЃЉЃЌЕуC1ЕФзјБъЮЊЃЈЉ3ЃЌ2ЃЉЃЌдђЕуBЕФзјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉвдЕуAЮЊЮЛЫЦжааФЃЌдкЭјИёЭМжазїЁїAB2C2ЃЌЪЙЁїAB2C2КЭЁїABCЮЛЫЦЃЌЧвЮЛЫЦБШЮЊ1ЃК2ЃЛ
ЃЈ3ЃЉдкЭМЩЯБъГіЁїABCгыЁїA1B1C1ЕФЮЛЫЦжааФPЃЌВЂаДГіЕуPЕФзјБъЮЊЁЁ ЁЁЃЌМЦЫуЫФБпаЮABCPЕФжмГЄЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛДЮКЏЪ§y=mx+2ЕФЭМЯѓОЙ§ЕуЃЈЉ2ЃЌ6ЃЉЃЎ
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉЛГіДЫКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ3ЃЉЦНвЦДЫКЏЪ§ЕФЭМЯѓЃЌЪЙЕУЫќгыСНзјБъжсЫљЮЇГЩЕФЭМаЮЕФУцЛ§ЮЊ4ЃЌЧыжБНгаДГіДЫЪБЭМЯѓЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
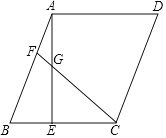
ЁОЬтФПЁПдкABCDжаЃЌAEЁЭBCгкЕуEЃЌFЮЊABБпЩЯвЛЕуЃЌСЌНгCFЃЌНЛAEгкЕуGЃЌCFЃНCBЃНAEЃЎ
ЃЈ1ЃЉШєAB![]() ЃЌBC
ЃЌBC![]() ЃЌЧѓCEЕФГЄЃЛ
ЃЌЧѓCEЕФГЄЃЛ
ЃЈ2ЃЉЧѓжЄЃКBEЃНCGЉAGЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌOBЪЧЁЯAOCЕФЦНЗжЯпЃЌODЪЧЁЯCOEЕФЦНЗжЯпЃЎ
(1)ШєЁЯAOBЃН50ЁуЃЌЁЯDOEЃН35ЁуЃЌЧѓЁЯBODЕФЖШЪ§ЃЛ
(2)ШєЁЯAOEЃН160ЁуЃЌЁЯCODЃН40ЁуЃЌЧѓЁЯAOBЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫБЃЛЄЛЗОГЃЌФГПЊЗЂЧјзлКЯжЮРэжИЛгВПОіЖЈЙКТђAЃЌBСНжжаЭКХЕФЮлЫЎДІРэЩшБИЙВ10ЬЈЃЎвбжЊгУ90ЭђдЊЙКТђAаЭКХЕФЮлЫЎДІРэЩшБИЕФЬЈЪ§гыгУ75ЭђдЊЙКТђBаЭКХЕФЮлЫЎДІРэЩшБИЕФЬЈЪ§ЯрЭЌЃЌУПЬЈЩшБИМлИёМАдТДІРэЮлЫЎСПШчЯТБэЫљЪОЃК
ЮлЫЎДІРэЩшБИ | AаЭ | BаЭ |
МлИёЃЈЭђдЊ/ЬЈЃЉ | m | m-3 |
дТДІРэЮлЫЎСПЃЈЖж/ЬЈЃЉ | 220 | 180 |
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉгЩгкЪмзЪН№ЯожЦЃЌжИЛгВПгУгкЙКТђЮлЫЎДІРэЩшБИЕФзЪН№ВЛГЌЙ§165ЭђдЊЃЌЮЪгаЖрЩйжжЙКТђЗНАИЃПВЂЧѓГіУПдТзюЖрДІРэЮлЫЎСПЕФЖжЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com