
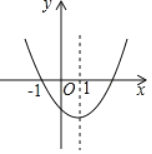
【题目】如图,是二次函数y=ax2+bx+c的图象,下列结论:①abc>0;②2a+b<0;③![]() <1,④a+c>0,其中正确的结论为_____(请把正确结论的序号都填在横线上)
<1,④a+c>0,其中正确的结论为_____(请把正确结论的序号都填在横线上)
【答案】①③
【解析】
由抛物线的开口方向判断a与0的关系,由对称轴的位置判断b与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
①∵由抛物线的开口方向向上,
∴a>0,
∵对称轴在y轴右侧,
∴a、b异号,即b<0,
∵抛物线与y轴的交点在y轴的负半轴上,
∴c<0,
故abc>0,
故①正确;
②由图象可知:对称轴![]() ,所以2a+b=0,
,所以2a+b=0,
故②不正确;
③由图象可知:抛物线与x轴有两个交点,
∴![]()
∴![]()
∴![]()
故③正确;
④由图象可知:当x=1时,y=0,
∴ab+c=0,
∵b=2a,
∴a+2a+c=0,
3a+c=0;
∵a>0,
∴a+c<0,
故④不正确.
综上可得:①③正确.
故答案为:①③.


科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线BD=1,∠ABC=120°,∠A、∠C所对的边记为a、c.
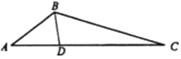
(1)当c=2时,求a的值;
(2)求△ABC的面积(用含a,c的式子表示即可);
(3)求证:a,c之和等于a,c之积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生环保意识,某中学举办了环保知识竞赛,某班共有5名学生(3名男生,2名女生)获奖.
(1)老师若从获奖的5名学生中选取一名作为班级的“环保小卫士”,则恰好是男生的概率为 .
(2)老师若从获奖的5名学生中任选两名作为班级的“环保小卫士”,请用画树状图法或列表法,求出恰好是一名男生、一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌毛衣和衬衫2016年9月至2017年4月在怀柔京北大世界的销量统计图![]() 根据统计图提供的信息,下列推断不合理的是
根据统计图提供的信息,下列推断不合理的是![]()
![]()

A. 9月毛衣的销量最低,10月衬衫的销量最高
B. 与10月相比,11月时,毛衣的销量有所增长,衬衫的销量有所下降
C. 9月![]() 月毛衣和衬衫的销量逐月增长
月毛衣和衬衫的销量逐月增长
D. 2月毛衣的销售量是衬衫销售量的7倍左右
查看答案和解析>>
科目:初中数学 来源: 题型:
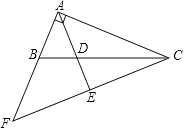
【题目】直角三角形ABC中,![]() ,D是斜边BC上一点,且
,D是斜边BC上一点,且![]() ,过点C作
,过点C作![]() ,交AD的延长线于点E,交AB延长线于点F.
,交AD的延长线于点E,交AB延长线于点F.
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,
,![]() ,过点B作
,过点B作![]() 于点G,连接
于点G,连接![]() 依题意补全图形,并求四边形ABGD的面积.
依题意补全图形,并求四边形ABGD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ACB=90°,AC=2,CB=4.点P为线段CB上一动点,连接AP,△APC与△APC′关于直线AP对称,其中点C的对称点为点C′.直线m过点A且平行于CB
(1)如图①:连接AB,当点C落在线段AB上时,求BC′的长;
(2)如图②:当PC=![]() BC时,延长PC′交直线m于点D,求△ADC′面积;
BC时,延长PC′交直线m于点D,求△ADC′面积;
(3)在(2)的条件下,连接BC′,直接写出线段BC′的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
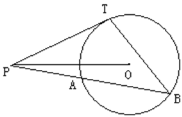
【题目】已知:如图,点P是半径为5cm的⊙O外的一点,OP= 13cm,PT切⊙O于T点,过点P作PB(PB>PA),设PA= x,PB= y。
(1)求y与x的函数解析式,并确定自变量x的取值范围;
(2)这个函数有最大值吗?若有求出此时△PBT的面积,若没有,请说明理由;
(3)是否存在这样的PB,使得![]() ,若存在,请求出PA的值,若不存在,请说明理由.
,若存在,请求出PA的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com