
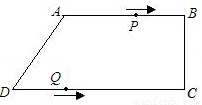
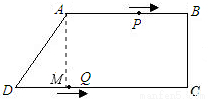
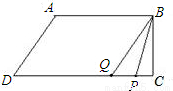
如图,在直角梯形ABCD中,AB∥CD,∠BCD=Rt∠,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
(1)16;(2)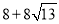 ;(3)
;(3)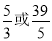 .
.
【解析】
试题分析:(1)过点A作AM⊥CD于M,根据勾股定理,可以求出DM=6所以DC=16.
(2)当四边形PBQD为平行四边形时,点P在AB上,点Q在DC上,如图示,由题可得:BP=10-3t,DQ=2t,所以可以列出方程10-3t=2t,解得t=2,此时,BP=DQ=4,CQ=12,在△CBQ中,根据勾股定理,求出BQ即可.
(3)此题要分三种情况进行讨论:即①当点P在线段AB上,②当点P在线段BC上,③当点P在线段CD上,根据三种情况点的位置,可以确定t的值.
(1)如图,过点A作AM⊥CD于M,
根据勾股定理,AD=10,AM=BC=8,
∴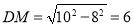 .∴CD=16.
.∴CD=16.
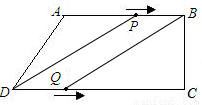
(2)当四边形PBQD为平行四边形时,
点P在AB上,点Q在DC上,如图,
由题知:BP=10-3t,DQ=2t,∴10-3t=2t,解得t=2.
此时,BP=DQ=4,CQ=12,∴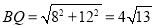 .
.
∴四边形PBQD的周长=2(BP+BQ)=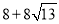 .
.
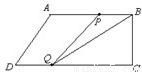
(3)①当点P在线段AB上时,即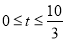 时,如图,
时,如图,
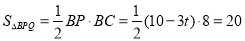 ,解得
,解得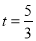 .
.
②当点P在线段BC上时,即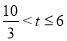 时,如图,BP=3t-10,CQ=16-2t,
时,如图,BP=3t-10,CQ=16-2t,
∴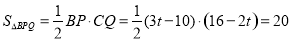 ,化简得:3t2-34t+100=0,△=-44<0,
,化简得:3t2-34t+100=0,△=-44<0,
∴方程无实数解.
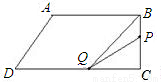
③当点P在线段CD上时,
若点P在Q的右侧,即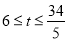 ,则有PQ=34-5t,
,则有PQ=34-5t,
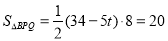 ,解得
,解得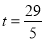 <6,舍去.
<6,舍去.
若点P在Q的左侧,即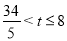 ,则有PQ=5t-34,
,则有PQ=5t-34,
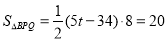 ,解得
,解得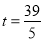 .
.
综上所述,满足条件的t存在,其值分别为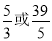 .
.
考点:1.双动点问题;2.平行四边形的性质;3.一元二次方程的应用;4.直角梯形的性质;5.勾股定理;6.分类思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2015届浙江省八年级4月质量检测数学试卷(解析版) 题型:解答题
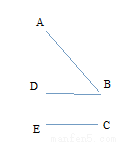
已知:如图:架在消防车上的云梯AB的坡比为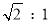 ,云梯AB的长为
,云梯AB的长为 m,云梯底部离地面1.5m(即BC=1.5m).求云梯顶端离地面的距离AE.
m,云梯底部离地面1.5m(即BC=1.5m).求云梯顶端离地面的距离AE.
查看答案和解析>>
科目:初中数学 来源:2015届浙江省温州市六校八年级下学期期中联考数学试卷(解析版) 题型:选择题
如图所示,O为 ABCD两对角线的交点,图中全等的三角形有( )
ABCD两对角线的交点,图中全等的三角形有( )

A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
科目:初中数学 来源:2015届浙江省八年级下学期期中考试数学试卷(解析版) 题型:选择题
若点P(a,2)与Q(-1,b)关于坐标原点对称,则a,b分别为( )
A.-1,2 B.1,-2 C.1,2 D.-1,-2
查看答案和解析>>
科目:初中数学 来源:2015届浙江省台州市八年级下学期期中考试数学试卷(解析版) 题型:解答题
如图,在菱形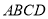 中,
中,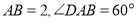 ,
,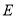 是边
是边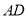 的中点,
的中点,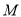 是边
是边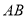 上任一点(不与点
上任一点(不与点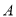 重合)延长
重合)延长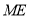 交
交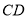 的延长线于点
的延长线于点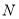 ,连结
,连结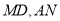 .
.
(1)求证: 四边形
四边形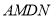 是平行四边形.
是平行四边形.
(2)当 为何值时,四边形
为何值时,四边形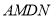 是矩形?请说明理由.
是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2015届河南省郑州市八年级下学期期末考试数学试卷(解析版) 题型:选择题
已知a<b,则下列不等式一定成立的是( )
A.a+3>b+3 B.2a>2b C.﹣a<﹣b D.a﹣b<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com