
分析 本题就是考查了1、2、6、26所有组合的和差(除去负数外)共有多少种情况,有多少不同的结果就有多少种称重克数.
解答 解:(1)当一端放砝码,另一端不放砝码时:
①当天平一端只放一个砝码时,可称量重物的克数有:1克,2克,6克,26克4种;
②当天平的一端只放两个砝码时,当天平一端只放一个砝码时,可称量重物的克数有:1+2=3克,1+6=7克,1+26=27克,2+6=8克,2+26=28克,6+26=32克6种;
③当天平一端只放三个砝码时,可称量重物的克数有:1+2+6=9克,1+2+26=29克,1+6+26=33课,2+6+26=34克共4种;
④当天平一端放四个砝码时,可称量重物的克数有1+2+6+26=35克共1种
(2)当两端都放砝码时:
①当两端都有一个砝码时,可称量的重物的克数有:2-1=1克,6-1=5克,6-2=4克,26-1=25克,26-1=24克,26-6=20克除去和上面重复的外,共5种;
②当两端共有三个砝码时,可称量的重物的克数有:6+1-2=5克,6+2-1=7克,1+26-2=25克,2+26-1=27克,26+1-6=22克,6+26-2=30克,26+1-6=21克,26+6-1=31克,26-1-2=23克,26-1-6=19克,26-2-6=18克除去重复的外,共有7种
③当天平两端放四个砝码时,可称量重物的克数有:26+1+2-6=23克,26+2+6-1=33克,26+1+6-2=31克,26+1-2-6=19克,26+2-1-6=21克,26+6-1-2=29克,26-1-2-6=17克除重复的外共1种.
所以共有4+6+4+1+5+7+1=28(种)
故答案为:28.
点评 此题主要考查了分类讨论的思想.解题过程中注意不重不漏.


科目:初中数学 来源: 题型:填空题
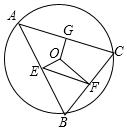 如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O,分别作AB、BC、AC的垂线,垂足分别为E、F、G,连接EF,若OG=3,则EF为4.
如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O,分别作AB、BC、AC的垂线,垂足分别为E、F、G,连接EF,若OG=3,则EF为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在平静的湖水中用的时间少 | B. | 在流动的河水中用的时间少 | ||
| C. | 两种情况所用时间相等 | D. | 以上均有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 0 | 3 |
| y | 2 | 0 |
| A. | k=2,b=3 | B. | k=-$\frac{2}{3}$,b=2 | C. | k=3,b=2 | D. | k=1,b=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知:如图在△ABC,△ADE中,∠BAC=∠DAE+90°,AB=AC,AD=AE.点C,D,E三点在同一条直线上,连接BD,BE.以下两个结论:
已知:如图在△ABC,△ADE中,∠BAC=∠DAE+90°,AB=AC,AD=AE.点C,D,E三点在同一条直线上,连接BD,BE.以下两个结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
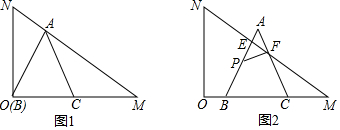
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com