
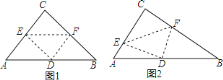
【题目】在![]() 中,
中,![]() ,翻折
,翻折![]() ,使点
,使点![]() 落在斜边
落在斜边![]() 上某一点
上某一点![]() 处,折痕为
处,折痕为![]() (点
(点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上)
上)
![]() 当
当![]() 时,若
时,若![]() 与
与![]() 相似(如图
相似(如图![]() ),求
),求![]() 的长;
的长;
![]() 当点
当点![]() 是
是![]() 的中点时(如图
的中点时(如图![]() ),
),![]() 与
与![]() 相似吗?请说明理由.
相似吗?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析
,理由见解析
【解析】
(1)如图1,连接CD,由已知条件得到△ABC是等腰直角三角形由于△CEF与△ABC相似,于是得到△CEF也是等腰直角三角形求得∠CEF=∠A=45°,于是得到EF∥AB,由轴对称的性质等等EF⊥CD,求出CD⊥AB,根据直角三角形的性质即可得到结论;
(2)如图2,连接CD,与EF交于点Q,根据直角三角形的性质得到CD=DB=![]() AB,于是得到∠DCB=∠B,由轴对称的性质得到∠CQF=∠DQF=90°,推出∠DCB+∠CFE=90°,由于∠B+∠A=90°,于是得到∠CFE=∠A,即可得到结论.
AB,于是得到∠DCB=∠B,由轴对称的性质得到∠CQF=∠DQF=90°,推出∠DCB+∠CFE=90°,由于∠B+∠A=90°,于是得到∠CFE=∠A,即可得到结论.
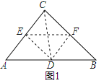
![]() 如图
如图![]() ,连接
,连接![]() ,
,
∵![]() ,
,
∴![]() 是等腰直角三角形
是等腰直角三角形
又∵![]() 与
与![]() 相似,
相似,
∴![]() 也是等腰直角三角形
也是等腰直角三角形
∴![]() ,
,
∴![]() ,
,
由轴对称的性质知:![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴点![]() 是
是![]() 的中点,
的中点,
∴![]() ;
;
![]() 当点
当点![]() 是
是![]() 的中点时,
的中点时,![]() 与
与![]() 相似,
相似,
理由如下:如图![]() ,连接
,连接![]() ,与
,与![]() 交于点
交于点![]() ,
,
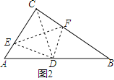
∵![]() 是
是![]() 的中线,
的中线,
∴![]() ,
,
∴![]() ,
,
由轴对称的性质可知,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】.鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组
“鞋码”与鞋长换算的对应数值:[注:“鞋码”是表示鞋子大小的一种号码]
鞋长(cm) | 16 | 19 | 21 | 24 |
鞋码(号) | 22 | 28 | 32 | 38 |
(1)设鞋长为x,“鞋码”为y,试判断点(x,y)在你学过的哪种函数的图象上?
(2)求x、y之间的函数关系式;(3)如果某人穿44号“鞋码”的鞋,那么他的鞋长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() 在反比例函数
在反比例函数![]() 的图象上,且点
的图象上,且点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]()
![]() .过点
.过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,且
,且![]() 的面积为
的面积为![]() .
.
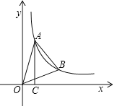
![]() 求该反比例函数的解析式;
求该反比例函数的解析式;
![]() 若
若![]() ,设直线
,设直线![]() 的解析式为
的解析式为![]() ,当
,当![]() 满足什么条件,
满足什么条件,![]() ?
?
![]() 求
求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
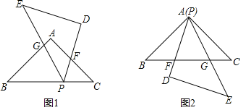
【题目】如图,![]() 、
、![]() 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,![]() .
.
![]() 若将
若将![]() 的顶点
的顶点![]() 放在
放在![]() 上(如图
上(如图![]() ),
),![]() 、
、![]() 分别与
分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() .求证:
.求证:![]() ;
;
![]() 若使
若使![]() 的顶点
的顶点![]() 与顶点
与顶点![]() 重合(如图
重合(如图![]() ),
),![]() 、
、![]() 与
与![]() 相交于点
相交于点![]() 、
、![]() .试问
.试问![]() 与
与![]() 还相似吗?为什么?
还相似吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
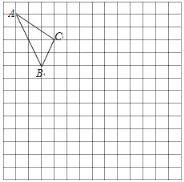
【题目】如图,在正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系(直接在图中画出);
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)写出点A1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移10cm,如图2,OA边与圆的两个交点对应CD的长为40cm则可知井盖的直径是( )
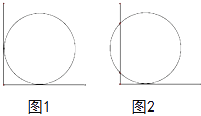
A. 25cm B. 30cm C. 50cm D. 60cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:在平面直角坐标系中,将一个图形先关于y轴对称,再向下平移2个单位记为1次“R变换”.如图,已知△ABC的三个顶点均在格点上,其中点B的坐标为(1,2).

(1)画出△ABC经过1次“R变换”后的图形△A1B1C1;
(2)若△ABC经过3次“R变换”后的图形为△A3B3C3,则顶点A3坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com