
分析 (1)根据题意可得出销量乘以每台利润进而得出总利润,进而得出答案;
(2)根据销量乘以每台利润进而得出总利润,即可求出即可.
解答 解:(1)y=$\left\{\begin{array}{l}{40x-20x=20x(0≤x≤10,且x为整数)}\\{[40-20-0.2(x-10)]x=-0.2{x}^{2}+22x(10<x≤100,且x为整数)}\end{array}\right.$;
(2)在0≤x≤10时,y=20x,当x=10时,y有最大值200;
在10<x≤100时,y=-0.2x2+22x,
当x=55时,y取得最大值=1210元,
∴顾客一次购买55件时,该网站从中获利最多,最大利润是1210元.
点评 此题主要考查了二次函数的应用,根据题意得出y与x的函数关系是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1000•sinα米 | B. | $\frac{1000}{sinα}$米 | C. | 1000•cosα米 | D. | $\frac{1000}{cosα}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:在△ABC中,D、E为AC、AB上的点,BD、CE相交于O,取AB的中点F,联结OF,若AD=$\frac{1}{2}$CD,AE=$\frac{1}{2}$BE
已知:在△ABC中,D、E为AC、AB上的点,BD、CE相交于O,取AB的中点F,联结OF,若AD=$\frac{1}{2}$CD,AE=$\frac{1}{2}$BE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
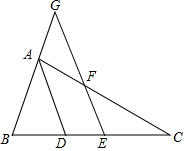 如图,△ABC中,AD平分∠BAC,EF交BA延长线于点G,∠CFE=∠G.
如图,△ABC中,AD平分∠BAC,EF交BA延长线于点G,∠CFE=∠G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
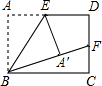 如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD=2$\sqrt{2}$.
如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD=2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两人在一段笔直的公路AB上行走,甲从A地出发前往B地,乙从B地出发前往A地,已知A、B两地相距4千米,乙比甲晚出发20分钟,甲、乙两人离A地的距离y(千米)与甲出发后经过的时间x(分钟)之间的函数关系如图所示.
甲、乙两人在一段笔直的公路AB上行走,甲从A地出发前往B地,乙从B地出发前往A地,已知A、B两地相距4千米,乙比甲晚出发20分钟,甲、乙两人离A地的距离y(千米)与甲出发后经过的时间x(分钟)之间的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com