
【题目】如图,直线y=-![]() x-
x-![]() 与x,y两轴分别交于A,B两点,与反比例函数y=
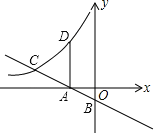
与x,y两轴分别交于A,B两点,与反比例函数y=![]() 的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
【答案】![]()
【解析】
作CH⊥x轴于H,如图,先利用一次函数解析式确定B(0,-![]() ),A(-3,0),再利用三角函数的定义计算出∠OAB=30°,则∠CAH=30°,设D(-3,t),则AC=AD=t,接着表示出CH=
),A(-3,0),再利用三角函数的定义计算出∠OAB=30°,则∠CAH=30°,设D(-3,t),则AC=AD=t,接着表示出CH=![]() AC=
AC=![]() t,AH=
t,AH=![]() CH=
CH=![]() t得到C(-3-
t得到C(-3-![]() t,
t,![]() t),然后利用反比例函数图象上点的坐标特征得到(-3-
t),然后利用反比例函数图象上点的坐标特征得到(-3-![]() t)
t)![]() t=3t,最后解方程即可.
t=3t,最后解方程即可.
作CH⊥x轴于H,如图,

当x=0时,y=-![]() x-
x-![]() =-
=-![]() ,则B(0,-
,则B(0,-![]() ),
),
当y=0时,-![]() x-
x-![]() =0,解得x=-3,则A(-3,0),
=0,解得x=-3,则A(-3,0),
∵tan∠OAB=![]() ,
,
∴∠OAB=30°,
∴∠CAH=30°,
设D(-3,t),则AC=AD=t,
在Rt△ACH中,CH=![]() AC=
AC=![]() t,AH=
t,AH=![]() CH=
CH=![]() t,
t,
∴C(-3-![]() t,
t,![]() t),
t),
∵C、D两点在反比例函数图象上,
∴(-3-![]() t)
t)![]() t=3t,解得t=2
t=3t,解得t=2![]() ,
,
即D点的纵坐标为2![]() .
.
故答案为2![]() .
.


科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在数轴上点A,B所对应的数是-4,4.
![]()
对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于-4,则称代数式N是线段AB的封闭代数式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的封闭代数式.
问题:
(1)关于x代数式|x-1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值和最小值分别是____ ______.
所以代数式|x-1|__________(填是或不是)线段AB的封闭代数式.
(2)以下关x的代数式:
①![]() ;②x2+1;③x2+|x|-8;④|x+2|-|x-1|-1.
;②x2+1;③x2+|x|-8;④|x+2|-|x-1|-1.
是线段AB的封闭代数式是__________,并证明(只需要证明是线段AB的封闭代数式的式子,不是的不需证明).
(![]() )关于x的代数式
)关于x的代数式![]() 是线段AB的封闭代数式,则有理数a的最大值是__________,最小值是__________.
是线段AB的封闭代数式,则有理数a的最大值是__________,最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
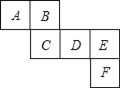
【题目】如图是一个正方体的表面展开图,请回答下列问题:
(1)与面B、C相对的面分别是 ;
(2)若A=a3+a2b+3,B=a2b﹣3,C=a3﹣1,D=﹣(a2b﹣6),且相对两个面所表示的代数式的和都相等,求E、F分别代表的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC中,AB=AC,∠BAC=![]() ,点A、B分别在x轴和y轴上,点C的坐标为(6,2).
,点A、B分别在x轴和y轴上,点C的坐标为(6,2).
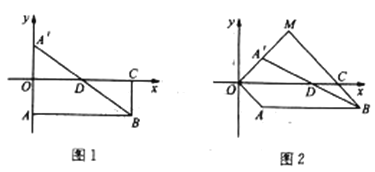
(1)如图1,求A点坐标;
(2)如图2,延长CA至点D,使得AD=AC,连接BD,线段BD交x轴于点E,问:在x轴上是否存在点M,使得△BDM的面积等于△ABO的面积,若存在,求点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 坐标为
坐标为![]() ,以原点
,以原点![]() 为顶点的四边形
为顶点的四边形![]() 是平行四边形,将边
是平行四边形,将边![]() 沿
沿![]() 轴翻折得到线段
轴翻折得到线段![]() ,连结
,连结![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)如图1,当点![]() 在
在![]() 轴上,且其坐标为
轴上,且其坐标为![]() .
.
①求![]() 所在直线的函数表达式;
所在直线的函数表达式;
②求证:点![]() 为线段
为线段![]() 的中点;
的中点;
(2)如图2,当![]() 时,
时,![]() ,
,![]() 的延长线相交于点
的延长线相交于点![]() ,试求
,试求![]() 的值.(直接写出答案,不必说明理由)
的值.(直接写出答案,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家支持大学生创新办实业,提供小额无息贷款,学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额-成本=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生体育锻炼,某校八年级进行了体育测试,为了解女生体育测试情况,从中抽取了若干名女生的体育测试成绩.
a.体育委员小李在整理频数分布表时,不小心污染了统计表:
分组(分) | 频数 | 频数 |
21<x≤22 | 8 | 0.200 |
22<x≤23 | 4 | n |
23<x≤24 | 7 | 0.175 |
24<x≤25 | 3 | 0.075 |
25<x≤26 | 2 | 0.050 |
26<x≤27 | 8 | 0.200 |
27<x≤28 | m | 0.150 |
28<x≤29 | 2 | 0.050 |
合计 |
|
b.根据频数分布表,绘制如下频数分布直方图:
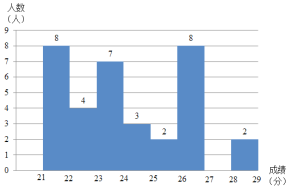
c.在此次测试中,共测试了800米,篮球,仰卧起坐,成绩统计如下:
项目 | 平均分 | 中位数 | 众数 |
800米 | 8.27 | 8.5 | 8.5 |
仰卧起坐 | 7.61 | 8 | 7.5 |
篮球 | 8.69 | 9 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m,n的值;
(2)补全直方图;
(3)请结合C中统计图表,给该校女生体育训练提供建议(至少从两个不同的角度分析).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,射线OC在∠A0B的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“定分线”
(1)一个角的平分线______这个角的“定分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=![]() ,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
(3)如图2,若∠MPN=45°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成90°时停止旋转,旋转的时间为t秒.同时射线PM绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止.当PQ是∠MPN的“定分线”时,求t的值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com