
ШчЙћШ§НЧаЮгавЛБпЩЯЕФжаЯпГЄЧЁКУЕШгкетБпЕФГЄЃЌФЧУДГЦетИіШ§НЧаЮЮЊЁАКУЭцШ§НЧаЮЁБЃЎ
ЃЈ1ЃЉЧыгУжБГпКЭдВЙцЛвЛИіЁАКУЭцШ§НЧаЮЁБЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌtanA= 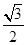 ЃЌЧѓжЄЃКЁїABCЪЧЁАКУЭцШ§НЧаЮЁБЃЛ
ЃЌЧѓжЄЃКЁїABCЪЧЁАКУЭцШ§НЧаЮЁБЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌвбжЊСтаЮABCDЕФБпГЄЮЊaЃЌЁЯABC=2ІТЃЌЕуPЃЌQДгЕуAЭЌЪБГіЗЂЃЌвдЯрЭЌЫйЖШЗжБ№биелЯпABЉBCКЭADЉDCЯђжеЕуCдЫЖЏЃЌМЧЕуPОЙ§ЕФТЗГЬЮЊsЃЎ
ЂйЕБІТ=45ЁуЪБЃЌШєЁїAPQЪЧЁАКУЭцШ§НЧаЮЁБЃЌЪдЧѓ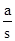 ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкЕБtanІТЕФШЁжЕдкЪВУДЗЖЮЇФкЃЌЕуPЃЌQдкдЫЖЏЙ§ГЬжаЃЌгаЧвжЛгавЛИіЁїAPQФмГЩЮЊЁАКУЭцШ§НЧаЮЁБЃЎЧыжБНгаДГіtanІТЕФШЁжЕЗЖЮЇЃЎ
ЃЈ4ЃЉвРОнЃЈ3ЃЉЕФЬѕМўЃЌЬсГівЛИіЙигкЁАдкЕуPЃЌQЕФдЫЖЏЙ§ГЬжаЃЌtanІТЕФШЁжЕЗЖЮЇгыЁїAPQЪЧЁЎКУЭцШ§НЧаЮЁЏЕФИіЪ§ЙиЯЕЁБЕФецУќЬтЃЈЁАКУЭцШ§НЧаЮЁБЕФИіЪ§ЯоЖЈВЛФмЮЊ1ЃЉ
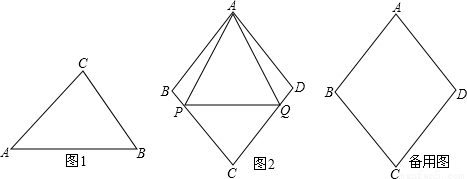
ЃЈ1ЃЉМћНтЮі ЃЈ2ЃЉМћНтЮі ЃЈ3ЃЉЂй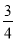 Ђк
Ђк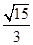 ЃМtanІТЃМ2
ЃМtanІТЃМ2
ЃЈ4ЃЉдкPЁЂQЕФдЫЖЏЙ§ГЬжаЃЌЕБ0ЃМtanІТЃМ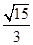 ЪБЃЌЪЙЕУЁїAPQГЩЮЊЁАКУЭцШ§НЧаЮЁБЕФИіЪ§ЮЊ2ЃЎ
ЪБЃЌЪЙЕУЁїAPQГЩЮЊЁАКУЭцШ§НЧаЮЁБЕФИіЪ§ЮЊ2ЃЎ
ЁОНтЮіЁПЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1ЃЌ
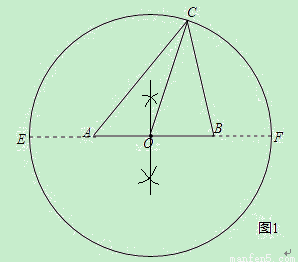
ЂйзївЛЬѕЯпЖЮABЃЌ
ЂкзїЯпЖЮABЕФжаЕуOЃЌ
ЂлвдЕуOЮЊдВаФЃЌABГЄЮЊАыОЖЛдВЃЌ
ЂмдкдВOЩЯШЁвЛЕуCЃЈЕуEЁЂFГ§ЭтЃЉЃЌСЌНгACЁЂBCЃЎ
ЁрЁїABCЪЧЫљЧѓзїЕФШ§НЧаЮЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌ
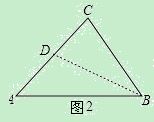
ШЁACЕФжаЕуDЃЌСЌНгBDЃЎ
ЁпЁЯC=90ЁуЃЌtanA=  ЃЌ
ЃЌ
Ёр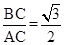
ЁрЩшBC= 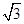 xЃЌдђAC=2xЃЌ
xЃЌдђAC=2xЃЌ
ЁпDЪЧACЕФжаЕуЃЌ
ЁрCD= 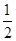 AC=x
AC=x
ЁрBD= 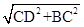 =
= 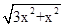 =2xЃЌ
=2xЃЌ
ЁрAC=BD
ЁрЁїABCЪЧЁАКУЭцШ§НЧаЮЁБЃЛ
ЃЈ3ЃЉЂйЕБІТ=45ЁуЃЌЕуPдкABЩЯЪБЃЌ
ЁрЁЯABC=2ІТ=90ЁуЃЌ
ЁрЁїAPQЪЧЕШбќжБНЧШ§НЧаЮЃЌВЛПЩФмЪЧЁАКУЭцШ§НЧаЮЁБЃЌ
ШчЭМ3ЃЌЕБPдкBCЩЯЪБЃЌСЌНгACНЛPQгкЕуEЃЌбгГЄABНЛQPЕФбгГЄЯпгкЕуFЃЌ
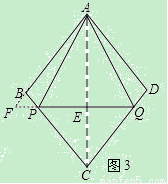
ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯABC=2ІТ=90ЁуЃЌ
ЁрЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрAB=BCЃЌЁЯACB=ЁЯACD=45ЁуЃЌ
ЁрЁЯCAB=ЁЯACPЃЌ
ЁпPC=CQЃЌЁЯACB=ЁЯACDЃЌ
ЁрЁЯAEF=ЁЯCEP=90ЁуЃЌ
ЁрЁїAEFЁзЁїCEPЃЌЧвЁїAEFЁЂЁїCEPКЭЁїBFPЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌ
Ёр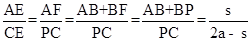 ЃЎ
ЃЎ
ЁпPE=CEЃЌ
Ёр ЃЎ
ЃЎ
ЃЈЂёЃЉЕБЕзБпPQгыЫќЕФжаЯпAEЯрЕШЪБЃЌМДAE=PQЪБЃЌ
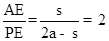 ЃЌ
ЃЌ
Ёр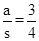 ЃЌ
ЃЌ
ЃЈЂђЃЉЕБбќAPгыЫќЕФжаЯпQMЯрЕШЃЌМДAP=QMЪБЃЌ
зїQNЁЭAPгкNЃЌШчЭМ4

ЁпAP=QM=AQ
ЁрMN=AN= 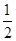 MPЃЎ
MPЃЎ
ЁрQN= 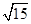 MNЃЌ
MNЃЌ
ЁрtanЁЯAPQ= 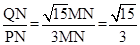 ЃЌ
ЃЌ
ЁрtanЁЯAPE= 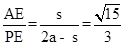 ЃЌ
ЃЌ
Ёр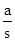 =
= 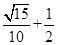
ЂкгЩЂйПЩжЊЃЌЕБAE=PQКЭAP=QMЪБЃЌгаЧвжЛгавЛИіЁїAPQФмГЩЮЊЁАКУЭцШ§НЧаЮЁБЃЌ
Ёр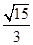 ЃМtanІТЃМ2ЪБЃЌгаЧвжЛгавЛИіЁїAPQФмГЩЮЊЁАКУЭцШ§НЧаЮЁБЃЎ
ЃМtanІТЃМ2ЪБЃЌгаЧвжЛгавЛИіЁїAPQФмГЩЮЊЁАКУЭцШ§НЧаЮЁБЃЎ
ЃЈ4ЃЉгЩЃЈ3ЃЉПЩвджЊЕРЃКдкPЁЂQЕФдЫЖЏЙ§ГЬжаЃЌЕБ0ЃМtanІТЃМ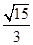 ЪБЃЌЪЙЕУЁїAPQГЩЮЊЁАКУЭцШ§НЧаЮЁБЕФИіЪ§ЮЊ2ЃЎ
ЪБЃЌЪЙЕУЁїAPQГЩЮЊЁАКУЭцШ§НЧаЮЁБЕФИіЪ§ЮЊ2ЃЎ
ЃЈ1ЃЉЯШЛвЛЬѕЯпЖЮABЃЌдйШЗЖЈABЕФжаЕуOЃЌвдЕуOЮЊдВаФЃЌABЮЊАыОЖЛдВЃЌдкдВOЩЯШЁвЛЕуCЃЌСЌНгACЁЂBCЃЌдђЁїABCЪЧЫљЧѓзїЕФШ§НЧаЮЃЛ
ЃЈ2ЃЉШЁACЕФжаЕуDЃЌСЌНгBDЃЌЩшBC= 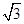 xЃЌИљОнЬѕМўПЩвдЧѓГіAC=2xЃЌгЩШ§НЧКЏЪ§ПЩвдЧѓГіBD=2xЃЌДгЖјЕУГіAC=BDЃЌДгЖјЕУГіНсТлЃЛ
xЃЌИљОнЬѕМўПЩвдЧѓГіAC=2xЃЌгЩШ§НЧКЏЪ§ПЩвдЧѓГіBD=2xЃЌДгЖјЕУГіAC=BDЃЌДгЖјЕУГіНсТлЃЛ
ЃЈ3ЃЉЂйЕБІТ=45ЁуЪБЃЌЗжЧщПіЬжТлЃЌPЕудкABЩЯЪБЃЌЁїAPQЪЧЕШбќжБНЧШ§НЧаЮЃЌВЛПЩФмЪЧЁАКУЭцШ§НЧаЮЁБЃЌЕБPдкBCЩЯЪБЃЌбгГЄABНЛQPЕФбгГЄЯпгкЕуFЃЌПЩвдЧѓГі ЃЌдйЗжЧщПіЬжТлЃЌЕБAE=PQКЭAP=QMЪБЃЌЧѓГі
ЃЌдйЗжЧщПіЬжТлЃЌЕБAE=PQКЭAP=QMЪБЃЌЧѓГі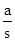 ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкИљОнЂйЧѓГіЕФСНИі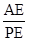 ЕФжЕПЩвдЧѓГіtanІТЕФШЁжЕЗЖЮЇЃЛ
ЕФжЕПЩвдЧѓГіtanІТЕФШЁжЕЗЖЮЇЃЛ
ЃЈ4ЃЉгЩЃЈ3ЃЉПЩвдЕУГіЁАдкPЁЂQЕФдЫЖЏЙ§ГЬжаЃЌЕБ0ЃМtanІТЃМ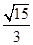 ЪБЃЌЪЙЕУЁїAPQГЩЮЊЁЎКУЭцШ§НЧаЮЁЏЕФИіЪ§ЮЊ2ЁБЪЧецУќЬтЃЎ
ЪБЃЌЪЙЕУЁїAPQГЩЮЊЁЎКУЭцШ§НЧаЮЁЏЕФИіЪ§ЮЊ2ЁБЪЧецУќЬтЃЎ


 зпНјЮФбдЮФЯЕСаД№АИ
зпНјЮФбдЮФЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014НьЩНЖЋЪЁЬЉАВЪаЬЉЩНЧјГѕШ§ЯТбЇЦкЦкФЉЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ШчЭМЃЌвбжЊAB=ADЃЌФЧУДЬэМгЯТСавЛИіЬѕМўКѓЃЌШдЮоЗЈХаЖЈЁїABCЁеЁїADCЕФЪЧЃЈЁЁЁЁЃЉ
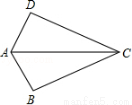
AЃЎCB=CD BЃЎЁЯBAC=ЁЯDAC
CЃЎЁЯBCA=ЁЯDCA DЃЎЁЯB=ЁЯD=90Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014жаПМУћЪІЭЦМіЪ§бЇИХТЪЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
ШчЭМЃЌЕкЃЈ1ЃЉИіЭМга1ИіКкЧђЃЛЕкЃЈ2ЃЉИіЭМЮЊ3ИіЭЌбљДѓаЁЧђЕўГЩЕФЭМаЮЃЌзюЯТвЛВуЕФ2ИіЧђЮЊКкЩЋЃЌЦфгрЮЊАзЩЋЃЛЕкЃЈ3ЃЉИіЭМЮЊ6ИіЭЌбљДѓаЁЧђЕўГЩЕФЭМаЮЃЌзюЯТвЛВуЕФ3ИіЧђЮЊКкЩЋЃЌЦфгрЮЊАзЩЋЃЛЁЃЛдђДгЕкЃЈnЃЉИіЭМжаЫцЛњШЁГівЛИіЧђЃЌЪЧКкЧђЕФИХТЪЪЧЁЁЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014жаПМУћЪІЭЦМіЪ§бЇЪ§ЕФЙцТЩЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
вбжЊ123456789101112Ё997998999ЪЧгЩСЌајећЪ§1жС999ХХСазщГЩЕФвЛИіЪ§ЃЌдкИУЪ§жаДгзѓЭљгвЪ§Ек2013ЮЛЩЯЕФЪ§зжЮЊЁЁ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014жаПМУћЪІЭЦМіЪ§бЇЪ§аЮНсКЯЫМЯыЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
дквЛЬѕБЪжБЕФЙЋТЗЩЯгаAЁЂBСНЕиЃЌМзЦяздааГЕДгAЕиЕНBЕиЃЛввЦяздааГЕДгBЕиЕНAЕиЃЌЕНДяAЕиКѓСЂМДАДдТЗЗЕЛиЃЌШчЭМЪЧМзЁЂввСНШЫОрBЕиЕФОрРыyЃЈkmЃЉгыааЪЛЪБМфxЃЈhЃЉжЎМфЕФКЏЪ§ЭМЯѓЃЌИљОнЭМЯѓНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉаДГіAЁЂBСНЕижЎМфЕФОрРыЃЛ
ЃЈ2ЃЉЧѓГіЕуMЕФзјБъЃЌВЂНтЪЭИУЕузјБъЫљБэЪОЕФЪЕМЪвтвхЃЛ
ЃЈ3ЃЉШєСНШЫжЎМфБЃГжЕФОрРыВЛГЌЙ§3kmЪБЃЌФмЙЛгУЮоЯпЖдНВЛњБЃГжСЊЯЕЃЌЧыжБНгаДГіМзЁЂввСНШЫФмЙЛгУЮоЯпЖдНВЛњБЃГжСЊЯЕЪБxЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014жаПМУћЪІЭЦМіЪ§бЇГпЙцзїЭМЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ШчЭМЃЌдкИјЖЈЕФвЛеХЦНааЫФБпаЮжНЦЌЩЯзївЛИіСтаЮЃЎМзЁЂввСНШЫЕФзїЗЈШчЯТЃК
МзЃКСЌНгACЃЌзїACЕФДЙжБЦНЗжЯпMNЗжБ№НЛADЃЌACЃЌBCгкMЃЌOЃЌNЃЌСЌНгANЃЌCMЃЌдђЫФБпаЮANCMЪЧСтаЮЃЎ
ввЃКЗжБ№зїЁЯAЃЌЁЯBЕФЦНЗжЯпAEЃЌBFЃЌЗжБ№НЛBCЃЌADгкEЃЌFЃЌСЌНгEFЃЌдђЫФБпаЮABEFЪЧСтаЮЃЎ
ИљОнСНШЫЕФзїЗЈПЩХаЖЯЃЈЁЁЁЁЃЉ

AЃЎМзе§ШЗЃЌввДэЮѓ BЃЎвве§ШЗЃЌМзДэЮѓ
CЃЎМзЁЂввОље§ШЗ DЃЎМзЁЂввОљДэЮѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014жаПМУћЪІЭЦМіЪ§бЇЪЕЪ§ЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ШчЭМЃЌдкЪ§жсЩЯБэЪО-1ЃЌ- ЕФЖдгІЕуЮЊAЃЌBЃЌШєЕуAЪЧЯпЖЮBCЕФжаЕуЃЌдђЕуCБэЪОЕФЪ§ЮЊЃЈ ЃЉ
ЕФЖдгІЕуЮЊAЃЌBЃЌШєЕуAЪЧЯпЖЮBCЕФжаЕуЃЌдђЕуCБэЪОЕФЪ§ЮЊЃЈ ЃЉ

AЃЎ BЃЎ
BЃЎ
CЃЎ DЃЎ
DЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014жаПМУћЪІЭЦМіЪ§бЇдВЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ШчЭМЃЌDCЪЧЁбOжБОЖЃЌЯвABЁЭCDгкFЃЌСЌНгBCЃЌDBЃЌдђЯТСаНсТлДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ

AЃЎ
BЃЎAF=BF
CЃЎOF=CF
DЃЎЁЯDBC=90Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014жаПМУћЪІЭЦМіЪ§бЇвђЪНЗжНтЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
дкЪЕЪ§ЗЖЮЇФкЗжНтвђЪНЃКx4Љ9=ЁЁ ЁЁЃЌx2Љ2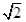 x+2=ЁЁ ЃЎ
x+2=ЁЁ ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com