练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，DC是⊙O直径，弦AB⊥CD于F，连接BC，DB，则下列结论错误的是（　　）

    A．

    B．AF=BF

    C．OF=CF

    D．∠DBC=90°

     

    C

    【解析】根据垂径定理可判断A、B，根据圆周角定理可判断D，继而可得出答案．

    【解析】
    ∵DC是⊙O直径，弦AB⊥CD于F，

    ∴点D是优弧AB的中点，点C是劣弧AB的中点，

    A、，正确，故本选项错误；

    B、AF=BF，正确，故本选项错误；

    C、OF=CF，不能得出，错误，故本选项符合题意；

    D、∠DBC=90°，正确，故本选项错误；

    故选C．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014中考名师推荐数学点、线、面、角（解析版） 题型：填空题

    如图，四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B=       ．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014中考名师推荐数学展示定义、规则（解析版） 题型：解答题

    如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”．

    （1）请用直尺和圆规画一个“好玩三角形”；

    （2）如图1，在Rt△ABC中，∠C=90°，tanA= 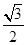，求证：△ABC是“好玩三角形”；

    （3）如图2，已知菱形ABCD的边长为a，∠ABC=2β，点P，Q从点A同时出发，以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动，记点P经过的路程为s．

    ①当β=45°时，若△APQ是“好玩三角形”，试求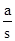的值；

    ②当tanβ的取值在什么范围内，点P，Q在运动过程中，有且只有一个△APQ能成为“好玩三角形”．请直接写出tanβ的取值范围．

    （4）依据（3）的条件，提出一个关于“在点P，Q的运动过程中，tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题（“好玩三角形”的个数限定不能为1）

     

     

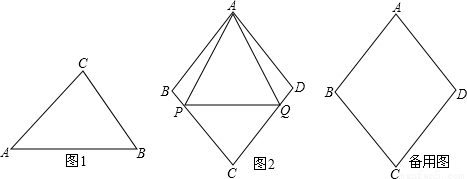
    查看答案和解析>>

    科目：初中数学 来源：2014中考名师推荐数学圆（解析版） 题型：填空题

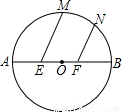
    如图，已知⊙O的直径AB=6，E、F为AB的三等分点，M、N为上两点，且∠MEB=∠NFB=60°，则EM+FN=　　．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014中考名师推荐数学圆（解析版） 题型：选择题

    如图．Rt△ABC内接于⊙O，BC为直径，AB=4，AC=3，D是的中点，CD与AB的交点为E，则等于（　　）

    A．4       B．3.5       C．3       D．2.8

     

    查看答案和解析>>

    科目：初中数学 来源：2014中考名师推荐数学圆（解析版） 题型：选择题

    已知⊙O1的半径是3cm，⊙O2的半径是2cm，O1O2=cm，则两圆的位置关系是（　　）

    A．相离

    B．外切

    C．相交

    D．内切

     

    查看答案和解析>>

    科目：初中数学 来源：2014中考名师推荐数学图形的规律（解析版） 题型：选择题

    将图1的正方形作如下操作：第1次：分别连接各边中点如图2，得到5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到9个正方形…，以此类推，根据以上操作，若要得到2013个正方形，则需要操作的次数是（　　）

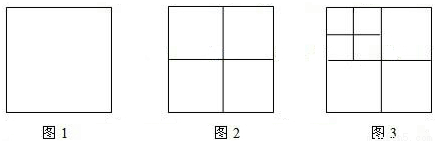
    A．502 B．503 C．504 D．505

     

    查看答案和解析>>

    科目：初中数学 来源：2014中考名师推荐数学图形的对称、平移与旋转（解析版） 题型：解答题

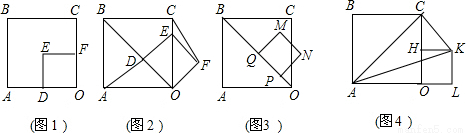
    如图1，把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起．

    （1）操作1：固定正方形OABC，将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF，如图2，连接AD、CF，线段AD与CF之间有怎样的数量关系？试证明你的结论；

    （2）操作2，如图2，将正方形ODEF沿着射线DB以每秒1个单位的速度平移，平移后的正方形ODEF设为正方形PQMN，如图3，设正方形PQMN移动的时间为x秒，正方形PQMN与正方形OABC的重叠部分面积为y，直接写出y与x之间的函数解析式；

    （3）操作3：固定正方形OABC，将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL，如图4，求△ACK的面积．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014中考名师推荐数学函数基础知识（解析版） 题型：选择题

    函数y=中，自变量x的取值范围是（　　）

    A．x＞-3

    B．x≥-3

    C．x≠-3

    D．x≤-3

     

    查看答案和解析>>

    同步练习册答案