
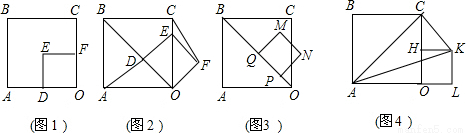
如图1,把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起.
(1)操作1:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
(2)操作2,如图2,将正方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
(3)操作3:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL,如图4,求△ACK的面积.
(1)相等 见解析 (2)见解析 (3)8
【解析】【解析】
(1)相等
由旋转的性质得∠AOB=∠COF,
在△AOD和△COF中,
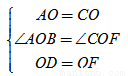
∴△AOD≌△COF(SAS),
∴AD=CF;
(2)①当0≤x≤4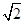 ﹣4时,y=22﹣
﹣4时,y=22﹣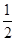 (2﹣x)2=﹣
(2﹣x)2=﹣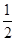 x2+2x+2;
x2+2x+2;
②当4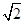 ﹣4≤x≤2时,y=22﹣
﹣4≤x≤2时,y=22﹣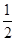 (2﹣x)2﹣
(2﹣x)2﹣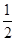 (4+x﹣4
(4+x﹣4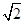 )2;
)2;
③2≤x≤4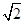 ﹣2时,y=22﹣
﹣2时,y=22﹣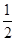 (4+x﹣4
(4+x﹣4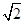 )2;
)2;
④4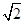 ﹣2≤x≤4
﹣2≤x≤4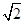 时,y=
时,y=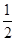 (4
(4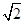 ﹣x)2
﹣x)2
⑤x≥4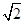 时,y=0.
时,y=0.
(3)连接OK,
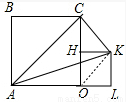
∵∠COK=∠ACO=45°,
∴OK∥AC,
∴S△ACK=S△AOC=8.
(1)根据旋转的性质得到∠AOB=∠COF,然后证得△AOD≌△COF后即可证得AD=CF;
(2)分当0≤x≤4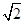 ﹣4时、当4
﹣4时、当4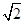 ﹣4≤x≤2时,2≤x≤4
﹣4≤x≤2时,2≤x≤4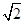 ﹣2时、4
﹣2时、4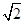 ﹣2≤x≤4
﹣2≤x≤4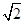 时、x≥4
时、x≥4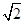 时五种情况列出两个变量之间的函数关系式即可;
时五种情况列出两个变量之间的函数关系式即可;
(3)连接OK,利用内错角相等得到OK∥AC,然后得到S△ACK=S△AOC=8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014中考名师推荐数学数的规律(解析版) 题型:填空题
已知123456789101112…997998999是由连续整数1至999排列组成的一个数,在该数中从左往右数第2013位上的数字为 .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
如图,DC是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )

A.
B.AF=BF
C.OF=CF
D.∠DBC=90°
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:填空题
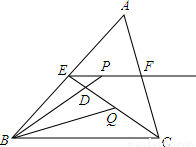
如图所示,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当CQ=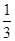 CE时,EP+BP=__________.
CE时,EP+BP=__________.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的折叠(解析版) 题型:填空题
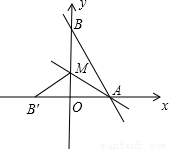
如图,直线y=﹣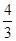 x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学分类讨论思想(解析版) 题型:填空题
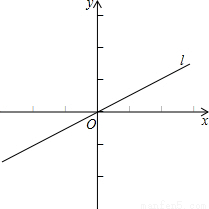
如图,在平面直角坐标系中,直线l经过原点O,且与x轴正半轴的夹角为30°,点M在x轴上,⊙M半径为2,⊙M与直线l相交于A,B两点,若△ABM为等腰直角三角形,则点M的坐标为 .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(二)(解析版) 题型:解答题
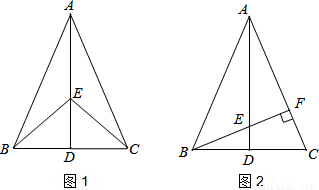
如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com