
点 P(a,a-3)在第四象限,则a的取值范围是 .
科目:初中数学 来源:2014中考名师推荐数学数的规律(解析版) 题型:选择题
把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现用等式AM=(i,j)表示正奇数M是第i组第j个数(从左往右数),如A7=(2,3),则A2013=( )
A.(45,77) B.(45,39)
C.(32,46) D.(32,23)
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
已知⊙O1的半径是3cm,⊙O2的半径是2cm,O1O2= cm,则两圆的位置关系是( )
cm,则两圆的位置关系是( )
A.相离
B.外切
C.相交
D.内切
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:选择题
直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( )
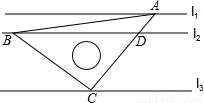
A.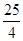 B.
B. C.
C.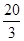 D.
D.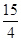
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的对称、平移与旋转(解析版) 题型:解答题
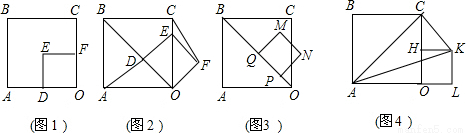
如图1,把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起.
(1)操作1:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
(2)操作2,如图2,将正方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
(3)操作3:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL,如图4,求△ACK的面积.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学四边形综合练习(解析版) 题型:解答题
如图①,在平行四边形ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B﹣A﹣D﹣A运动,沿B﹣A运动时的速度为每秒13个单位长度,沿A﹣D﹣A运动时的速度为每秒8个单位长度.点Q从点B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.
(1)当点P沿A﹣D﹣A运动时,求AP的长(用含t的代数式表示).
(2)连结AQ,在点P沿B﹣A﹣D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.
(3)过点Q作QR∥AB,交AD于点R,连结BR,如图②.在点P沿B﹣A﹣D运动过程中,当线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.
(4)设点C、D关于直线PQ的对称点分别为C′、D′,直接写出C′D′∥BC时t的值.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学分式(解析版) 题型:解答题
请写出一个同时满足下列条件的分式:
(1)分式的值不可能为0;
(2)分式有意义时,的取值范围是x≠±2;
(3)当x=0时,分式的值为-1.
你所写的分式为 .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(二)(解析版) 题型:填空题
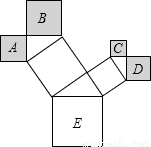
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,5,1,2.则最大的正方形E的面积是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com