
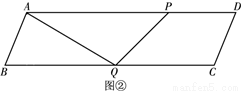
��ͼ������ƽ���ı���ABCD�У�AB=13��BC=50��BC���ϵĸ�Ϊ12����P�ӵ�B��������B��A��D��A�˶�����B��A�˶�ʱ���ٶ�Ϊÿ��13����λ���ȣ���A��D��A�˶�ʱ���ٶ�Ϊÿ��8����λ���ȣ���Q�ӵ�B������BC�����˶����ٶ�Ϊÿ��5����λ���ȣ�P��Q����ͬʱ����������Q�����Cʱ��P��Q����ͬʱֹͣ�˶������P���˶�ʱ��Ϊt���룩������PQ��
��1������P��A��D��A�˶�ʱ����AP�ij����ú�t�Ĵ���ʽ��ʾ����
��2������AQ���ڵ�P��B��A��D�˶������У�����P���B����A���غ�ʱ������APQ�����ΪS����S��t֮��ĺ�����ϵʽ��
��3������Q��QR��AB����AD�ڵ�R������BR����ͼ�����ڵ�P��B��A��D�˶������У����߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ�������ʱt��ֵ��
��4�����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬ֱ��д��C��D����BCʱt��ֵ��

��1������P��A��D�˶�ʱ��AP=8��t��1��=8t��8��
����P��D��A�˶�ʱ��AP=50��2��8��t��1��=108��8t��
��2��S=48t��48 ��3��t=1��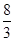 ��4��t=7��t=
��4��t=7��t=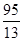 ��t=
��t=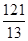
����������������
��1������P��A��D�˶�ʱ��AP=8��t��1��=8t��8��
����P��D��A�˶�ʱ��AP=50��2��8��t��1��=108��8t��
��2������P���A�غ�ʱ��BP=AB��t=1��
����P���D�غ�ʱ��AP=AD��8t��8=50��t=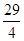 ��
��
��0��t��1ʱ����ͼ����

����Q��QE��AB��E��
S��ABQ= =
=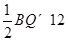 ��
��
��QE=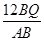 =
=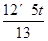 =
=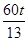 ��
��
��S��APQ=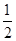 AP��EQ=
AP��EQ=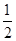 (13-13t����
(13-13t����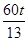 =��30t2+30t��
=��30t2+30t��
��1��t��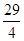 ʱ����ͼ����
ʱ����ͼ����
S= =
=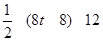 ��
��
��S=48t��48��
��3������P���R�غ�ʱ��
AP=BQ��8t��8=5t��t=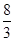 ��
��
��0��t��1ʱ����ͼ����

��S��BPM=S��BQM��
��PM=QM��
��AB��QR��
���PBM=��QRM����BPM=��MQR��
����BPM����RQM��
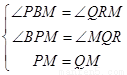
���BPM�ա�RQM��
��BP=RQ��
��RQ=AB��
��BP=AB
��13t=13��
��ã�t=1
��1��t��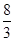 ʱ����ͼ����
ʱ����ͼ����

��BRƽ����Ӱ���������
��P���R�غϣ�
��t=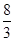 ��
��
��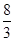 ��t��
��t��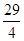 ʱ����ͼ����
ʱ����ͼ����
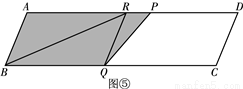
��S��ABR=S��QBR��
��S��ABR��S�ı���BQPR��
��BR���ܰ��ı���ABQP�ֳ������ȵ������֣�
������������t=1��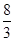 ʱ���߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ������֣�
ʱ���߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ������֣�
��4����ͼ������P��A��D֮���D��A֮��ʱ��C��D����BC�Ϸ���C��D����BCʱ��
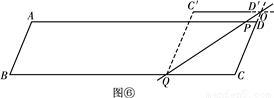
���C��OQ=��OQC��
�ߡ�C��OQ�ա�COQ��
���C��OQ=��COQ��
���CQO=��COQ��
��QC=OC��
��50��5t=50��8��t��1��+13����50��5t=8��t��1����50+13��
��ã�t=7��t=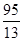 ��
��
��P��A��D֮���D��A֮�䣬C��D����BC�·���C��D����BCʱ����ͼ����

ͬ�������ε����ʿ��Եó���OD=PD��
��50��5t+13=8��t��1����50��
��ã�t=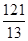 ��
��
����t=7��t=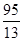 ��t=
��t=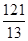 ʱ����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬��C��D����BC��
ʱ����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬��C��D����BC��
��1����������ۣ�����P��A��D�˶�ʱ������P��D��A�˶�ʱ�ֱ���Ա�ʾ��AP��ֵ��
��2���������ۣ���0��t��1ʱ����1��t��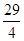 ʱ�����������ε������ʽ�ֱ����S��t�ĺ�����ϵʽ��
ʱ�����������ε������ʽ�ֱ����S��t�ĺ�����ϵʽ��
��3����������ۣ���0��t��1ʱ����1��t��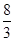 ʱ����
ʱ����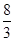 ��t��
��t��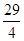 ʱ�����������ε������Ƚ������������⼴�ɣ�
ʱ�����������ε������Ƚ������������⼴�ɣ�
��4����������۵�P��A��D֮���D��A֮��ʱ����ͼ����������ԳƵ����ʿ���֪���ı���QCOC��Ϊ���Σ����������ʽ������������⣬��P��D��A֮����ͼ�����������ε����ʽ������������⼴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧ�߹���ͼ�������棩 ���ͣ�ѡ����
��ͼ���ڸ�����һ��ƽ���ı���ֽƬ����һ�����Σ��ס������˵��������£�
�ף�����AC����AC�Ĵ�ֱƽ����MN�ֱ�AD��AC��BC��M��O��N������AN��CM�����ı���ANCM�����Σ�
�ң��ֱ�����A����B��ƽ����AE��BF���ֱ�BC��AD��E��F������EF�����ı���ABEF�����Σ�
�������˵��������жϣ�������

A������ȷ���Ҵ��� B������ȷ���״���
C���ס��Ҿ���ȷ D���ס��Ҿ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧͼ�ε����ƣ������棩 ���ͣ������
��ͼ��ʾ���ڡ�ABC�У�BC=6��E��F�ֱ���AB��AC���е㣬����P������EF�ϣ�BP��CE��D����CBP��ƽ���߽�CE��Q����CQ=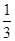 CEʱ��EP+BP=__________��
CEʱ��EP+BP=__________��
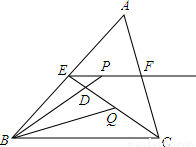
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧͼ�������꣨�����棩 ���ͣ������
�� P��a��a-3���ڵ������ޣ���a��ȡֵ��Χ������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧ��ʽ�ֽ⣨�����棩 ���ͣ������
��ʵ����Χ�ڷֽ���ʽ��x4��9=�� ����x2��2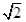 x+2=�� ��
x+2=�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧ�����������������棩 ���ͣ������
��ͼ����֪��A�ڷ���������y��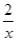 ��ͼ���ϣ���B��C�ֱ��ڷ���������y��
��ͼ���ϣ���B��C�ֱ��ڷ���������y��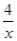 ��ͼ���ϣ���AB��x�ᣬAC��y�ᣬ��AB=2AC�����A������Ϊ��������
��ͼ���ϣ���AB��x�ᣬAC��y�ᣬ��AB=2AC�����A������Ϊ��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧ��������˼�루�����棩 ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�ֱ��l����ԭ��O������x��������ļн�Ϊ30������M��x���ϣ���M�뾶Ϊ2����M��ֱ��l�ཻ��A��B���㣬����ABMΪ����ֱ�������Σ����M������Ϊ�� ����
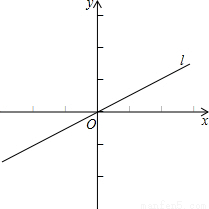
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧ�����Σ�һ���������棩 ���ͣ������
��ͼ��AB��CD�ཻ�ڵ�O��AC��CD�ڵ�C������BOD=38�㣬����A= .

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com