
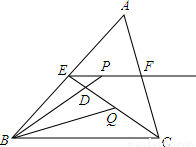
如图所示,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当CQ=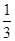 CE时,EP+BP=__________.
CE时,EP+BP=__________.
12
【解析】延长BQ交射线EF于M,根据三角形的中位线平行于第三边可得EF∥BC,根据两直线平行,内错角相等可得∠M=∠CBM,再根据角平分线的定义可得∠PBM=∠CBM,从而得到∠M=∠PBM,根据等角对等边可得BP=PM,求出EP+BP=EM,再根据CQ= CE求出EQ=2CQ,然后根据△MEQ和△BCQ相似,利用相似三角形对应边成比例列式求解即可.
CE求出EQ=2CQ,然后根据△MEQ和△BCQ相似,利用相似三角形对应边成比例列式求解即可.
【解析】
如图,延长BQ交射线EF于M,

∵E、F分别是AB、AC的中点,
∴EF∥BC,
∴∠M=∠CBM,
∵BQ是∠CBP的平分线,
∴∠PBM=∠CBM,
∴∠M=∠PBM,
∴BP=PM,
∴EP+BP=EP+PM=EM,
∵CQ= CE,
CE,
∴EQ=2CQ,
由EF∥BC得,△MEQ∽△BCQ,
∴ =
= =2,
=2,
∴EM=2BC=2×6=12,
即EP+BP=12.
故答案为:12.


科目:初中数学 来源:2014中考名师推荐数学整式(解析版) 题型:解答题
古希腊著名的毕达哥拉斯学派把1、3、6、10 …,这样的数称为“三角形数”,而把1、4、9、16…,这样的数称为“正方形数”.
(1)第5个三角形数是 ,第n个“三角形数”是 ,第5个“正方形数”是 ,第n个正方形数是 ;
(2)经探究我们发现:任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.
例如:①4=1+3,②9=3+6,③16=6+10,④ ,⑤ ,….
请写出上面第4个和第5个等式;
(3)在(2)中,请探究第n个等式,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:填空题
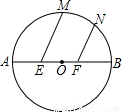
如图,已知⊙O的直径AB=6,E、F为AB的三等分点,M、N为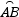 上两点,且∠MEB=∠NFB=60°,则EM+FN= .
上两点,且∠MEB=∠NFB=60°,则EM+FN= .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
已知⊙O1的半径是3cm,⊙O2的半径是2cm,O1O2= cm,则两圆的位置关系是( )
cm,则两圆的位置关系是( )
A.相离
B.外切
C.相交
D.内切
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的规律(解析版) 题型:选择题
将图1的正方形作如下操作:第1次:分别连接各边中点如图2,得到5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,根据以上操作,若要得到2013个正方形,则需要操作的次数是( )
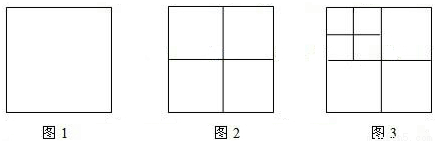
A.502 B.503 C.504 D.505
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:选择题
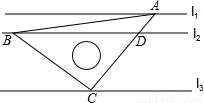
直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( )
A.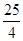 B.
B. C.
C.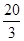 D.
D.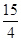
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的对称、平移与旋转(解析版) 题型:解答题
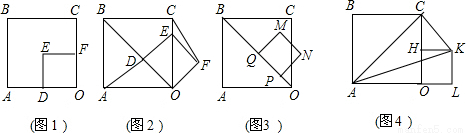
如图1,把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起.
(1)操作1:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
(2)操作2,如图2,将正方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
(3)操作3:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL,如图4,求△ACK的面积.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学四边形综合练习(解析版) 题型:解答题
如图①,在平行四边形ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B﹣A﹣D﹣A运动,沿B﹣A运动时的速度为每秒13个单位长度,沿A﹣D﹣A运动时的速度为每秒8个单位长度.点Q从点B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.
(1)当点P沿A﹣D﹣A运动时,求AP的长(用含t的代数式表示).
(2)连结AQ,在点P沿B﹣A﹣D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.
(3)过点Q作QR∥AB,交AD于点R,连结BR,如图②.在点P沿B﹣A﹣D运动过程中,当线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.
(4)设点C、D关于直线PQ的对称点分别为C′、D′,直接写出C′D′∥BC时t的值.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学二次函数(解析版) 题型:选择题
如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )

A. B.
B.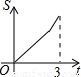 C.
C.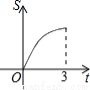 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com