
Ι≈œΘάΑ÷χΟϊΒΡ±œ¥οΗγά≠ΥΙ―ß≈…Α―1ΓΔ3ΓΔ6ΓΔ10 Γ≠Θ§’β―υΒΡ ΐ≥ΤΈΣΓΑ»ΐΫ«–Έ ΐΓ±Θ§ΕχΑ―1ΓΔ4ΓΔ9ΓΔ16Γ≠Θ§’β―υΒΡ ΐ≥ΤΈΣΓΑ’ΐΖΫ–Έ ΐΓ±Θ°
Θ®1Θ©ΒΎ5Ηω»ΐΫ«–Έ ΐ «ΓΓΓΓΘ§ΒΎnΗωΓΑ»ΐΫ«–Έ ΐΓ± «ΓΓΓΓΘ§ΒΎ5ΗωΓΑ’ΐΖΫ–Έ ΐΓ± «ΓΓΓΓΘ§ΒΎnΗω’ΐΖΫ–Έ ΐ «ΓΓ ΘΜ
Θ®2Θ©Ψ≠ΧΫΨΩΈ“Ο«ΖΔœ÷ΘΚ»ΈΚΈ“ΜΗω¥σ”Ύ1ΒΡΓΑ’ΐΖΫ–Έ ΐΓ±ΕΦΩ…“‘Ω¥ΉςΝΫΗωœύΝΎΓΑ»ΐΫ«–Έ ΐΓ±÷°ΚΆΘ°
άΐ»γΘΚΔΌ4=1+3Θ§ΔΎ9=3+6Θ§Δέ16=6+10Θ§ΔήΓΓ ΓΓΘ§ΔίΓΓ ΓΓΘ§Γ≠Θ°
«κ–¥≥ω…œΟφΒΎ4ΗωΚΆΒΎ5ΗωΒ» ΫΘΜ
Θ®3Θ©‘ΎΘ®2Θ©÷–Θ§«κΧΫΨΩΒΎnΗωΒ» ΫΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘ°
Θ®1Θ©15Θ§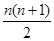 Θ§25Θ§n2ΘΜ
Θ§25Θ§n2ΘΜ
Θ®2Θ©25=10+15Θ§36=15+21ΘΜ
Θ®3Θ©ΦϊΫβΈω
ΓΨΫβΈωΓΩΘ®1Θ©Ιέ≤λΖΔœ÷Θ§ΒΎ5Ηω»ΐΫ«–Έ ΐΒ»”ΎΒΎ4Ηω»ΐΫ«–Έ ΐΦ”…œ5Θ§Φ¥ΈΣ15Θ§ΒΎnΗωΓΑ»ΐΫ«–Έ ΐΓ±Β»”ΎΒΎΘ®n©¹1Θ©ΗωΓΑ»ΐΫ«–Έ ΐΓ±Φ”…œnΘ§Φ¥ΈΣ1+2+3+Γ≠+nΘ§ΦΤΥψΦ¥Ω…ΘΜΒΎ5ΗωΓΑ’ΐΖΫ–Έ ΐΓ± «52Θ§ΒΎnΗω’ΐΖΫ–Έ ΐ «n2ΘΜ
Θ®2Θ©ΗυΨίΔΌ4=1+3Θ§ΔΎ9=3+6Θ§Δέ16=6+10Φ¥Ω…ΒΟ≥ωΒΎ4ΗωΒ» ΫΈΣΒΎ5Ηω»ΐΫ«–Έ ΐΒ»”ΎΒΎ4Ηω»ΐΫ«–Έ ΐΦ”…œΒΎ5Ηω»ΐΫ«–Έ ΐΘ§ΒΎ5ΗωΒ» ΫΈΣΒΎ6Ηω»ΐΫ«–Έ ΐΒ»”ΎΒΎ5Ηω»ΐΫ«–Έ ΐΦ”…œΒΎ6Ηω»ΐΫ«–Έ ΐΘΜ
Θ®3Θ©ΒΎnΗωΒ» ΫΈΣΒΎΘ®n+1Θ©ΗωΓΑ»ΐΫ«–Έ ΐΓ±Β»”ΎΒΎnΗωΓΑ»ΐΫ«–Έ ΐΓ±Φ”…œΒΎΘ®n+1Θ©ΗωΓΑ»ΐΫ«–Έ ΐΓ±Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©15Θ§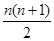 Θ§25Θ§n2ΘΜ
Θ§25Θ§n2ΘΜ
Θ®2Θ©25=10+15Θ§36=15+21ΘΜ
Θ®3Θ©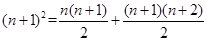 Θ§
Θ§
ΓΏ”“±Ώ=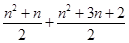
=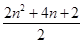
=n2+2n+1=Θ®n+1Θ©2=Ήσ±ΏΘ§
Γύ‘≠Β» Ϋ≥…ΝΔΘ°
Ι ¥πΑΗΈΣ15Θ§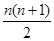 Θ§25Θ§n2ΘΜ25=10+15Θ§36=15+21Θ°
Θ§25Θ§n2ΘΜ25=10+15Θ§36=15+21Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ2014Ϋλ…ΫΕΪ ΓΧ©Α≤ –Χ©…Ϋ«χ≥θ»ΐœ¬―ßΤΎΤΎΡ© ΐ―ß ‘ΨμΘ®ΫβΈωΑφΘ© Χβ–ΆΘΚΫβ¥πΧβ
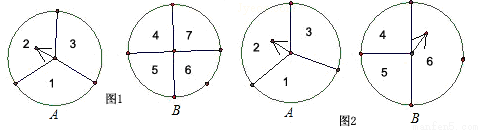
»γΆΦ1Θ§AΓΔBΝΫΗωΉΣ≈ΧΖ÷±π±ΜΖ÷≥…»ΐΗωΓΔΥΡΗωœύΆ§ΒΡ…»–ΈΘ§Ζ÷±πΉΣΕ·A≈ΧΓΔB≈ΧΗς“Μ¥ΈΘ®»τ÷Η’κ«ΓΚΟ÷Η‘ΎΖ÷ΗνœΏ…œΘ§‘ρ÷ΊΉΣ“Μ¥ΈΘ§÷±ΒΫ÷Η’κ÷Ηœρ“ΜΗω ΐΉ÷ΈΣ÷ΙΘ©Θ°
Θ®1Θ©”ΟΝ–±μΘ®ΜρΜ≠ ςΉ¥ΆΦΘ©ΒΡΖΫΖ®Θ§«σΝΫΗω÷Η’κΥυ÷ΗΒΡ«χ”ρΡΎΒΡ ΐΉ÷÷°ΚΆ¥σ”Ύ7ΒΡΗ≈¬ ΘΜ
Θ®2Θ©»γΙϊΫΪΆΦ1÷–ΒΡΉΣ≈ΧΗΡΈΣΆΦ2Θ§Τδ”ύ≤Μ±δΘ§«σΝΫΗω÷Η’κΥυ÷Η«χ”ρΒΡ ΐΉ÷÷°ΚΆ¥σ”Ύ7ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ2014÷–ΩΦΟϊ ΠΆΤΦω ΐ―ßΆ≥ΦΤΘ®ΫβΈωΑφΘ© Χβ–ΆΘΚ―Γ‘ώΧβ
Ρ≥–ΘΈΣΝΥΝΥΫβ―ß…ζΒΡ…μΧεΥΊ÷ «ιΩωΘ§Ε‘≥θ»ΐΘ®2Θ©ΑύΒΡ50Οϊ―ß…ζΫχ––ΝΥΝΔΕ®Χχ‘ΕΓΔ«Π«ρΓΔ100ΟΉ»ΐΗωœνΡΩΒΡ≤β ‘Θ§ΟΩΗωœνΡΩ¬ζΖ÷ΈΣ10Ζ÷Θ°»γΆΦΘ§ «ΫΪΗΟ―ß…ζΥυΒΟΒΡ»ΐœν≥…Φ®Θ®≥…Φ®ΨυΈΣ’ϊ ΐΘ©÷°ΚΆΫχ––’ϊάμΚσΘ§Ζ÷≥…5ΉιΜ≠≥ωΒΡΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ§“―÷Σ¥”Ήσ÷Ν”“«Α4Ηω–ΓΉιΒΡΤΒ¬ Ζ÷±πΈΣ0.02Θ§0.1Θ§0.12Θ§0.46Θ°
œ¬Ν–ΥΒΖ®ΘΚ
Θ®1Θ©―ß…ζΒΡ≥…Φ®Γί27Ζ÷ΒΡΙ≤”–15»ΥΘΜ
Θ®2Θ©―ß…ζ≥…Φ®ΒΡ÷Ύ ΐ‘ΎΒΎΥΡ–ΓΉιΘ®22.5ΓΪ26.5Θ©ΡΎΘΜ
Θ®3Θ©―ß…ζ≥…Φ®ΒΡ÷–ΈΜ ΐ‘ΎΒΎΥΡ–ΓΉιΘ®22.5ΓΪ26.5Θ©ΖΕΈßΡΎΘ°
Τδ÷–’ΐ»ΖΒΡΥΒΖ®”–Θ®ΓΓΓΓΘ©

AΘ°0Ηω BΘ°1Ηω CΘ°2Ηω DΘ°3Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ2014÷–ΩΦΟϊ ΠΆΤΦω ΐ―ßΒψΓΔœΏΓΔΟφΓΔΫ«Θ®ΫβΈωΑφΘ© Χβ–ΆΘΚ―Γ‘ώΧβ
»γΆΦΘ§OAΓΆOCΘ§OBΓΆODΘ§œ¬ΟφΫα¬έ÷–Θ§Τδ÷–ΥΒΖ®’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©

ΔΌΓœAOB=ΓœCODΘΜ
ΔΎΓœAOB+ΓœCOD=90ΓψΘΜ
ΔέΓœBOC+ΓœAOD=180ΓψΘΜ
ΔήΓœAOC-ΓœCOD=ΓœBOCΘ°
AΘ°ΔΌΔΎΔέ
BΘ°ΔΌΔΎΔή
CΘ°ΔΌΔέΔή
DΘ°ΔΎΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ2014÷–ΩΦΟϊ ΠΆΤΦω ΐ―ßΗ≈¬ Θ®ΫβΈωΑφΘ© Χβ–ΆΘΚΧνΩ’Χβ
»γΆΦΘ§ΒΎΘ®1Θ©ΗωΆΦ”–1ΗωΚΎ«ρΘΜΒΎΘ®2Θ©ΗωΆΦΈΣ3ΗωΆ§―υ¥σ–Γ«ρΒΰ≥…ΒΡΆΦ–ΈΘ§Ήνœ¬“Μ≤ψΒΡ2Ηω«ρΈΣΚΎ…ΪΘ§Τδ”ύΈΣΑΉ…ΪΘΜΒΎΘ®3Θ©ΗωΆΦΈΣ6ΗωΆ§―υ¥σ–Γ«ρΒΰ≥…ΒΡΆΦ–ΈΘ§Ήνœ¬“Μ≤ψΒΡ3Ηω«ρΈΣΚΎ…ΪΘ§Τδ”ύΈΣΑΉ…ΪΘΜΓ≠ΘΜ‘ρ¥”ΒΎΘ®nΘ©ΗωΆΦ÷–ΥφΜζ»Γ≥ω“ΜΗω«ρΘ§ «ΚΎ«ρΒΡΗ≈¬ «ΓΓΓΓΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ2014÷–ΩΦΟϊ ΠΆΤΦω ΐ―ß’ϊ ΫΘ®ΫβΈωΑφΘ© Χβ–ΆΘΚ―Γ‘ώΧβ
Ρ…ΟΉ «Ζ«≥Θ–ΓΒΡ≥ΛΕ»ΒΞΈΜΘ§“―÷Σ1Ρ…ΟΉ= 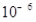 ΚΝΟΉΘ§Ρ≥÷÷≤ΓΕΨΒΡ÷±ΨΕΈΣ100Ρ…ΟΉΘ§»τΫΪ’β÷÷≤ΓΕΨ≈≈≥…1ΚΝΟΉ≥ΛΘ§‘ρ≤ΓΕΨΒΡΗω ΐ «Θ®ΓΓΓΓΘ©
ΚΝΟΉΘ§Ρ≥÷÷≤ΓΕΨΒΡ÷±ΨΕΈΣ100Ρ…ΟΉΘ§»τΫΪ’β÷÷≤ΓΕΨ≈≈≥…1ΚΝΟΉ≥ΛΘ§‘ρ≤ΓΕΨΒΡΗω ΐ «Θ®ΓΓΓΓΘ©
AΘ°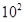 Ηω BΘ°
Ηω BΘ°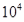 Ηω
Ηω
CΘ°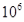 Ηω DΘ°
Ηω DΘ°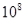 Ηω
Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ2014÷–ΩΦΟϊ ΠΆΤΦω ΐ―ß ΐΒΡΙφ¬…Θ®ΫβΈωΑφΘ© Χβ–ΆΘΚΧνΩ’Χβ
“―÷Σ123456789101112Γ≠997998999 «”…Ν§–χ’ϊ ΐ1÷Ν999≈≈Ν–Ήι≥…ΒΡ“ΜΗω ΐΘ§‘ΎΗΟ ΐ÷–¥”ΉσΆυ”“ ΐΒΎ2013ΈΜ…œΒΡ ΐΉ÷ΈΣΓΓ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ2014÷–ΩΦΟϊ ΠΆΤΦω ΐ―ß≥ΏΙφΉςΆΦΘ®ΫβΈωΑφΘ© Χβ–ΆΘΚ―Γ‘ώΧβ
»γΆΦΘ§‘ΎΗχΕ®ΒΡ“Μ’≈ΤΫ––ΥΡ±Ώ–Έ÷ΫΤ§…œΉς“ΜΗωΝβ–ΈΘ°ΦΉΓΔ““ΝΫ»ΥΒΡΉςΖ®»γœ¬ΘΚ
ΦΉΘΚΝ§Ϋ”ACΘ§ΉςACΒΡ¥Ι÷±ΤΫΖ÷œΏMNΖ÷±πΫΜADΘ§ACΘ§BC”ΎMΘ§OΘ§NΘ§Ν§Ϋ”ANΘ§CMΘ§‘ρΥΡ±Ώ–ΈANCM «Νβ–ΈΘ°
““ΘΚΖ÷±πΉςΓœAΘ§ΓœBΒΡΤΫΖ÷œΏAEΘ§BFΘ§Ζ÷±πΫΜBCΘ§AD”ΎEΘ§FΘ§Ν§Ϋ”EFΘ§‘ρΥΡ±Ώ–ΈABEF «Νβ–ΈΘ°
ΗυΨίΝΫ»ΥΒΡΉςΖ®Ω…≈–ΕœΘ®ΓΓΓΓΘ©

AΘ°ΦΉ’ΐ»ΖΘ§““¥μΈσ BΘ°““’ΐ»ΖΘ§ΦΉ¥μΈσ
CΘ°ΦΉΓΔ““Ψυ’ΐ»Ζ DΘ°ΦΉΓΔ““Ψυ¥μΈσ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ2014÷–ΩΦΟϊ ΠΆΤΦω ΐ―ßΆΦ–ΈΒΡœύΥΤΘ®ΫβΈωΑφΘ© Χβ–ΆΘΚΧνΩ’Χβ
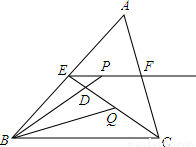
»γΆΦΥυ ΨΘ§‘ΎΓςABC÷–Θ§BC=6Θ§EΓΔFΖ÷±π «ABΓΔACΒΡ÷–ΒψΘ§Ε·ΒψP‘Ύ…δœΏEF…œΘ§BPΫΜCE”ΎDΘ§ΓœCBPΒΡΤΫΖ÷œΏΫΜCE”ΎQΘ§Β±CQ=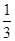 CE ±Θ§EP+BP=__________Θ°
CE ±Θ§EP+BP=__________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com