
ijУΪ���˽�ѧ������������������Գ�����2�����50��ѧ��������������Զ��Ǧ��100��������Ŀ�IJ��ԣ�ÿ����Ŀ����Ϊ10�֣���ͼ���ǽ���ѧ�����õ�����ɼ����ɼ���Ϊ������֮�ͽ��������ֳ�5�黭����Ƶ���ֲ�ֱ��ͼ����֪��������ǰ4��С���Ƶ�ʷֱ�Ϊ0.02��0.1��0.12��0.46��
����˵����
��1��ѧ���ijɼ���27�ֵĹ���15�ˣ�
��2��ѧ���ɼ��������ڵ���С�飨22.5��26.5���ڣ�
��3��ѧ���ɼ�����λ���ڵ���С�飨22.5��26.5����Χ�ڣ�
������ȷ��˵���У�������

A��0�� B��1�� C��2�� D��3��
C
�����������⿼���Ƶ���ֲ�ֱ��ͼ������������ͳ��ͼ��ȡ��Ϣ��������ͬʱ������λ����������������n�����ݣ�����С�����������nΪ������λ���м���Ǹ���������λ�������nΪż����λ���м���������ƽ����������λ�����κ�һ�����ݣ���һ��??����λ���ģ�����λ����һ�������������е���������һ�����ݣ����ִ��������Ǹ�������Ϊ�������ݵ�����������������ݵ�Ƶ�ʺ�Ϊ1��õ������Ƶ�ʣ�Ȼ����ÿ������=������������Ƶ�ʣ��õ�����������������жϣ�1���������������ĸ����ж�����������һ��С�飬���жϣ�2������������λ���ĸ�����жϣ�3��������
��������
��������ǰ5��С���Ƶ��֮��Ϊ1����ǰ�ĸ��ֱ�Ϊ0.02��0.1��0.12��0.46���ʵ������Ƶ����1-��0.02+0.1+0.12+0.46��=0.3��ѧ���ijɼ���27�ֵ��ڵ����飬�ܹ���50��ѧ�����ʵ����鹲��50��0.3=15�ˣ��ʣ�1����ȷ���۲�ֱ��ͼ��������������࣬��ѧ���ɼ���������һ���ڵ���С�飨22.5��26.5���ڣ��ʣ�2������ȷ����3��ѧ���ɼ�����λ���ǵ�25�����͵�26������ƽ������Ӧ�����ڵ����飬�ʣ�3����ȷ����ѡC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014������һ�����꼶������ĩ������ѧ�Ծ��������棩 ���ͣ������
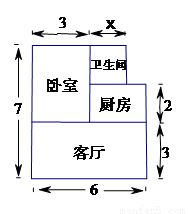
����������ɳƺ�ӹ���һ��С������Ʒ������ȥij¥���˽������֪, �û�����Ʒ���ĵ�����8000Ԫ/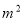 �������ͼ��ʾ����λ���ף�������Ŀ�δ�������Ϊ
�������ͼ��ʾ����λ���ף�������Ŀ�δ�������Ϊ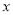 �ף����۷���Ϊ�������ṩ�����������Żݷ�����
�ף����۷���Ϊ�������ṩ�����������Żݷ�����
����һ�������ĵ�����8000Ԫ/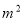 �����г������������
����������������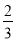 �������
�������
��������������ԭ�����ܽ���9�۳��ۣ�
��1����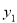 ��ʾ����һ�й���һ�û�����Ʒ�����ܽ���
��ʾ����һ�й���һ�û�����Ʒ�����ܽ���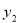 ��ʾ�������й���һ�û�����Ʒ�����ܽ��ֱ����
��ʾ�������й���һ�û�����Ʒ�����ܽ��ֱ����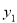 ��
��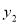 ��
��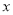 �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2����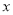 ȡ��ֵʱ�������Ż��������ܽ��һ���ࣿ
ȡ��ֵʱ�������Ż��������ܽ��һ���ࣿ
��3�����������ֽ�����2012��1���ڽ��н���9��Ԫס�������������Ϊ6�꣬�ӿ�ʼ�������һ���������³�����������������0.5%��ÿ�»�������=ƽ��ÿ��Ӧ���Ĵ��������+����Ϣ������Ϣ=������ʣ�������������������
�������������һ����Ӧ���������Ƕ���Ԫ��
�ڼ�����������ʲ��䣬���������ڽ����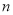 ��
��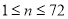 ��
�� �������������µĻ�������ΪP����д��P��
�������������µĻ�������ΪP����д��P�� ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014��ɽ��ʡ̩����̩ɽ��������ѧ����ĩ��ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ��һ�κ���y1=k1x+b��ͼ��ͷ���������y2= ��ͼ����A��1��2����B����2����1�����㣬��y1��y2����x��ȡֵ��Χ�ǣ�������
��ͼ����A��1��2����B����2����1�����㣬��y1��y2����x��ȡֵ��Χ�ǣ�������

A��x��1 B��x����2
C����2��x��0��x��1 D��x����2��0��x��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧת��˼�루�����棩 ���ͣ�ѡ����
��ͼ����Rt��ABC�У���B=90�㣬AB=3��BC=4����D��BC�ϣ���ACΪ�Խ��ߵ�������ADCE�У�DE����Сֵ�ǣ�������

A��2 B��3 C��4 D��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧͳ�ƣ������棩 ���ͣ������
ΪӦ��ȫ��Σ�����й�����Ͷ��40000��Ԫ��������������裬5��21�����ҷ���ί������40000��ԪͶ�ʹ��ɣ������������£���λ����Ԫ
�� �� Ͷ �� | �ʽ���� |
����ס���ȱ�����ס�� | 4000 |
ũ���������̺ͻ�����ʩ | 3700 |
��·���ش������ʩ����� ���е������� |
|
�����������������ҵ��չ | 1500 |
���ܼ��ź���̬���蹤�� | 2100 |
�������ºͲ�ҵ�ṹ���� | 3700 |
�봨�����ֺ�ָ��ؽ� |
|

�������ͳ��ͼ�������ṩ����Ϣ������������⣺
��1����ͳ�Ʊ��У�Ͷ����·���ش������ʩ����ͳ��е������족���ʽ�������� ����Ԫ��Ͷ���봨�����ֺ�ָ��ؽ������ʽ�������� ����Ԫ��
��2��������ͳ��ͼ�У��������������������ҵ��չ��������ռ�İٷ������� ���������ܼ��ź���̬���蹤�̡�������ռ�İٷ������� ����
��3��ͳ�Ʊ����ʽ���㡱��Ŀ�µ��߸������У���λ������ ����Ԫ���������� ����Ԫ��
��4��������ͳ��ͼ�У�������ס���ȱ�����ס����������ռ��Բ�Ľ�Ϊ �ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧ��ʽ�Ĺ��ɣ������棩 ���ͣ�ѡ����
��һ���������ܱ�ʾΪ������������ƽ���������������Ϊ���ǻ���������3=22��12��16=52��32������֪�ǻ�������С����˳���������У�
3��5��7��8��9��11��12��13��15��16��17��19��20��21��23��24��25������
���2006���ǻ����ǣ�������
A��2672 B��2675 C��2677 D��2680
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧ�㡢�ߡ��桢�ǣ������棩 ���ͣ������
��ͼ���ı���ABCD�У���M��N�ֱ���AB��BC�ϣ�����BMN��MN���ۣ�����FMN����MF��AD��FN��DC������B= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧ��ʽ�������棩 ���ͣ������
��ϣ�������ıϴ����˹ѧ�ɰ�1��3��6��10 ��������������Ϊ������������������1��4��9��16��������������Ϊ��������������
��1����5��������������������n������������������������5������������������������n�������������� ��
��2����̽�����Ƿ��֣��κ�һ������1�������������������Կ����������ڡ�����������֮�ͣ�
���磺��4=1+3����9=3+6����16=6+10������ �������� ��������
��д�������4���͵�5����ʽ��
��3���ڣ�2���У���̽����n����ʽ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�п���ʦ�Ƽ���ѧԲ�������棩 ���ͣ������
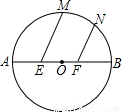
��ͼ����֪��O��ֱ��AB=6��E��FΪAB�����ȷֵ㣬M��NΪ �����㣬�ҡ�MEB=��NFB=60�㣬��EM+FN=������
�����㣬�ҡ�MEB=��NFB=60�㣬��EM+FN=������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com