
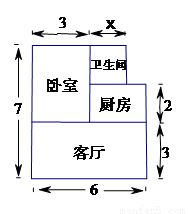
张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知, 该户型商品房的单价是8000元/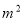 ,面积如图所示(单位:米,卫生间的宽未定,设宽为
,面积如图所示(单位:米,卫生间的宽未定,设宽为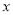 米),售房部为张先生提供了以下两种优惠方案:
米),售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是8000元/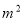 ,其中厨房可免费赠送
,其中厨房可免费赠送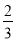 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售.
(1)用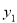 表示方案一中购买一套该户型商品房的总金额,用
表示方案一中购买一套该户型商品房的总金额,用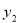 表示方案二中购买一套该户型商品房的总金额,分别求出
表示方案二中购买一套该户型商品房的总金额,分别求出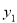 、
、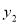 与
与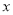 的关系式;
的关系式;
(2)求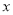 取何值时,两种优惠方案的总金额一样多?
取何值时,两种优惠方案的总金额一样多?
(3)张先生因现金不够,于2012年1月在建行借了9万元住房贷款,贷款期限为6年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月还款数额=平均每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率.
①张先生借款后第一个月应还款数额是多少元?
②假设贷款月利率不变,若张先生在借款后第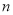 (
(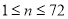 ,
, 是正整数)个月的还款数额为P,请写出P与
是正整数)个月的还款数额为P,请写出P与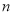 之间的关系式.
之间的关系式.
(1)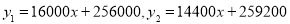 ;(2)x=2;(3)①1700,②P=-6.25n+1706.25.
;(2)x=2;(3)①1700,②P=-6.25n+1706.25.
【解析】
试题分析:(1)方案一:计算出卧室、客厅、卫生间的面积和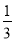 的厨房面积,再乘以单价即可;方案二:计算出整套房的面积×单价×90%即可;
的厨房面积,再乘以单价即可;方案二:计算出整套房的面积×单价×90%即可;
(2)依据两种优惠方案的总金额一样多列方程求解即可;
(3)①依据每月还款数额=平均每月应还的贷款本金数额+月利息列式计算即可;②依据每月还款数额=平
均每月应还的贷款本金数额+月利息列出多项式.
试题分析:(1) 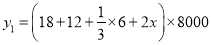 ,
,
=(32+2x)×8000,
=16000x+256000.
 ,
,
=(36+2x)×8000×0.9,
=14400x+259200.
故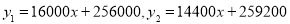 ;
;
(2)令(36+2x)×8000×0.9=(32+2x)×8000,
解得:x=2,
故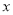 = 2时,两种优惠方案的总金额一样多;
= 2时,两种优惠方案的总金额一样多;
(3)①∵90000÷(6×12)=1250(元),
故张先生借款后第一个月应还款数额是1250+90000×0.5%=1250+450=1700(元);
②P=1250+[90000-(n-1)·1250] ×0.5%
=1250+450-6.25(n-1)
=1700-6.25(n-1)
=-6.25n+1706.25
故P与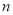 之间的关系式为P=-6.25n+1706.25.
之间的关系式为P=-6.25n+1706.25.
考点:1.一次函数;2.一元一次方程的应用.


科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:解答题
如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.
(1)求证:AC=CD.
(2)若AC=2,AO= ,求OD的长.
,求OD的长.

查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:选择题
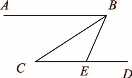
如图,已知AB∥CD,BC平分∠ABE,∠C= ,则∠BED 的度数是( )
,则∠BED 的度数是( )
A.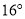 B.
B. C.
C.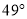 D.
D.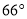
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,矩形OABC如图放置,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第5次碰到矩形的边时,点P的坐标为 ;当点P第2014次碰到矩形的边时,点P的坐标为____________.

查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:选择题
在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.众数 B.方差 C.平均数 D.中位数
查看答案和解析>>
科目:初中数学 来源:2014届重庆一中七年级上期期末考试数学试卷(解析版) 题型:填空题
某地居民生活用电基本价格为0.50元/度, 规定每月基本用电量为 度,超出部分电量的每度电价比基本用电量的每度电价高20%.某用户在5月份用电100度,共缴电费56元,则基本用电量
度,超出部分电量的每度电价比基本用电量的每度电价高20%.某用户在5月份用电100度,共缴电费56元,则基本用电量 是 度.
是 度.
查看答案和解析>>
科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:解答题
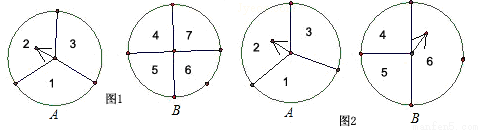
如图1,A、B两个转盘分别被分成三个、四个相同的扇形,分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止).
(1)用列表(或画树状图)的方法,求两个指针所指的区域内的数字之和大于7的概率;
(2)如果将图1中的转盘改为图2,其余不变,求两个指针所指区域的数字之和大于7的概率.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学统计(解析版) 题型:选择题
某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频数分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
下列说法:
(1)学生的成绩≥27分的共有15人;
(2)学生成绩的众数在第四小组(22.5~26.5)内;
(3)学生成绩的中位数在第四小组(22.5~26.5)范围内.
其中正确的说法有( )

A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com