
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)写出A、B两地之间的距离;
(2)求出点M的坐标,并解释该点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.

(1)30千米 (2)20千米 (3) ≤x≤
≤x≤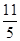 或
或 ≤x≤2
≤x≤2
【解析】【解析】
(1)x=0时,甲距离B地30千米,
所以,A、B两地的距离为30千米;
(2)由图可知,甲的速度:30÷2=15千米/时,
乙的速度:30÷1=30千米/时,
30÷(15+30)=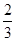 ,
,
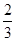 ×30=20千米,
×30=20千米,
所以,点M的坐标为(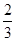 ,20),表示甲、乙两人出发
,20),表示甲、乙两人出发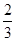 小时后相遇,此时距离B地20千米;
小时后相遇,此时距离B地20千米;
(3)设x小时甲、乙两人相距3km,
①若是相遇前,则15x+30x=30﹣3,
解得x= ,
,
②若是相遇后,则15x+30x=30+3,
解得x=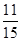 ,
,
③若是甲到达B地前,而乙到达A地后按原路返回时,
则15x﹣30(x﹣1)=3,
解得x= ,
,
所以,当 ≤x≤
≤x≤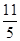 或
或 ≤x≤2时,甲、乙两人能够用无线对讲机保持联系.
≤x≤2时,甲、乙两人能够用无线对讲机保持联系.
(1)x=0时甲的y值即为A、B两地的距离;
(2)点M表示中途相遇时的情况,根据图象求出甲、乙两人的速度,进而求出相遇时间,然后求出乙的路程即可得到点M的坐标以及实际意义;
(3)分相遇前、相遇后和乙到达A地后按原路返回时三种情况求出x的值,然后写出取值范围即可.


科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:选择题
一元二次方程(x﹣2)=x(x﹣2)的解是( )
A.x=1 B.x=0 C.x1=2,x2=0 D.x1=2,x2=1
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学模型思想(解析版) 题型:解答题
阅读材料:
若a,b都是非负实数,则a+b≥ .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明:∵( )2≥0,∴a﹣
)2≥0,∴a﹣ +b≥0.
+b≥0.
∴a+b≥ .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:
已知x>0,求函数y=2x+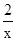 的最小值.
的最小值.
【解析】
y=2x+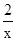 ≥
≥ =4.当且仅当2x=
=4.当且仅当2x=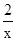 ,即x=1时,“=”成立.
,即x=1时,“=”成立.
当x=1时,函数有最小值,y最小=4.
问题解决:
汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油( +
+ )升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
)升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学展示定义、规则(解析版) 题型:解答题
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
(1)请用直尺和圆规画一个“好玩三角形”;
(2)如图1,在Rt△ABC中,∠C=90°,tanA= 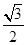 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点P经过的路程为s.
①当β=45°时,若△APQ是“好玩三角形”,试求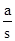 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1)
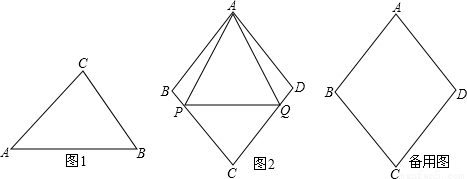
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学实数(解析版) 题型:解答题
(1)一个正数的平方根是a+3与2a﹣15,求a的值.
(2)已知 ,求
,求 的立方根.
的立方根.
(3)已知x、y为实数,且 .求
.求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是 的中点,CD与AB的交点为E,则
的中点,CD与AB的交点为E,则 等于( )
等于( )

A.4 B.3.5 C.3 D.2.8
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形与坐标(解析版) 题型:填空题
如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示).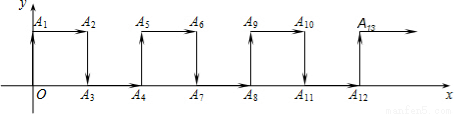
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com