Question

如图所示，△ABC是等腰三角形，且AC＝BC，∠ACB＝120°，在AB上取一点O，使OB＝OC，以O为圆心，OB为半径作圆，过C作CD∥AB交⊙O于点D，连接BD。

（1）猜想AC与⊙O的位置关系，并证明你的猜想；

（2）试判断四边形BOCD的形状，并证明你的判断；

（3）已知AC＝6，求扇形OBC围成的圆锥的底面圆半径。

 

 

Answer 1

（1）相切 （2）四边形BOCD是菱形 （3）∴底面圆半径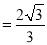

【解析】

试题分析：本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了菱形的判定方法和圆锥的计算．（1）根据等腰三角形的性质得∠A=∠ABC=30°，再由OB=OC得∠OCB=∠OBC=30°，所以∠ACO=∠ACB-∠OCB=90°，然后根据切线的判定定理即可得到，AC是⊙O的切线；

（2）连结OD，由CD∥AB得到∠AOC=∠OCD，根据三角形外角性质得∠AOC=∠OBC+∠OCB=60°，所以∠OCD=60°，于是可判断△OCD为等边三角形，则CD=OB=OC，先可判断四边形OBDC为平行四边形，加上OB=OC，于是可判断四边形BOCD为菱形；（3）在Rt△AOC中，根据含30度的直角三角形三边的关系得到

OC= 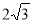∴弧BC的弧长= 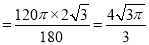然后根据圆锥的计算求圆锥的底面圆半径．

试题解析（1）AC与⊙O相切

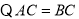，∠ACB＝120°，∴∠ABC＝∠A＝30°。

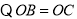，∠CBO＝∠BCO＝30°，

∴∠OCA＝120°－30°＝90°，∴AC⊥OC，

又∵OC是⊙O的半径，

∴AC与⊙O相切。

（2）四边形BOCD是菱形

连接OD。

∵CD∥AB，

∴∠OCD＝∠AOC＝2×30°＝60°

，

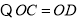∴△COD是等边三角形，

，

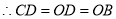∴四边形BOCD是平行四边形，

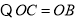
∴四边形BOCD是菱形。

（3）在Rt△AOC中，∠A＝30°，AC＝6，

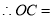ACtan∠A＝6tan30°＝，

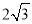∴弧BC的弧长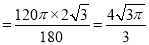

∴底面圆半径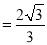

考点：切线的判定；菱形的判定；圆锥的计算．