
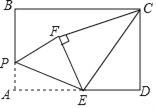
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为线段
为线段![]() 上一个动点,连接
上一个动点,连接![]() ,将
,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,连接
,连接![]() ,
,![]() ,当
,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_____.
的长为_____.
【答案】1或![]()
【解析】
分两种情况进行讨论:当∠CFE=90°时,△ECF是直角三角形;当∠CEF=90°时,△ECF是直角三角形,分别根据直角三角形的勾股定理列方程求解即可.
分两种情况讨论:
①当∠CFE=90°时,△ECF是直角三角形,如图1所示.由折叠可得:∠PFE=∠A=90°,AE=FE=DE,∴∠CFP=180°,即点P,F,C在一条直线上.
在Rt△CDE和Rt△CFE中,![]() ,∴Rt△CDE≌Rt△CFE(HL),∴CF=CD=4.
,∴Rt△CDE≌Rt△CFE(HL),∴CF=CD=4.
设AP=FP=x,则BP=4﹣x,CP=x+4.
在Rt△BCP中,BP2+BC2=PC2,即(4﹣x)2+62=(x+4)2,解得:x![]() ,即AP
,即AP![]() ;
;
②当∠CEF=90°时,△ECF是直角三角形,如图2所示,过F作FH⊥AB于H,作FQ⊥AD于Q,则∠FQE=∠D=90°.
又∵∠FEQ+∠CED=90°=∠ECD+∠CED,∴∠FEQ=∠ECD,∴△FEQ∽△ECD,∴![]() ,即
,即![]() ,解得:FQ
,解得:FQ![]() ,QE
,QE![]() ,∴AQ=HF
,∴AQ=HF![]() ,AH
,AH![]() ,设AP=FP=x,则HP
,设AP=FP=x,则HP![]() x.
x.
∵Rt△PFH中,HP2+HF2=PF2,即(![]() x)2+(
x)2+(![]() )2=x2,解得:x=1,即AP=1.
)2=x2,解得:x=1,即AP=1.
综上所述:AP的长为1或![]() .
.


科目:初中数学 来源: 题型:
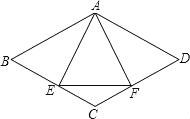
【题目】已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF;
(1)求证:△ABE≌△ADF.
(2)若菱形ABCD中,AB=4,∠C=120°,∠EAF=60°,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
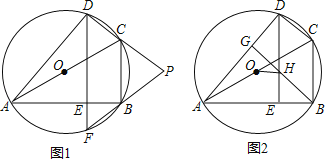
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛A,它周围8海里内有暗礁,渔船由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.
(1)求∠BAD的度数;
(2)如果渔船不改变航线继续向东航行,有没有触礁的危险?
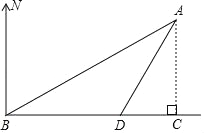
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() (a为常数)的图象与y轴相交于点A,与函数
(a为常数)的图象与y轴相交于点A,与函数![]() (x>0)的图象相交于点B(m,1).
(x>0)的图象相交于点B(m,1).
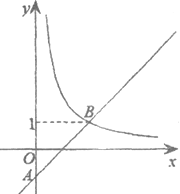
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求H点的坐标及k的值;
(2)点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;
(3)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
(x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
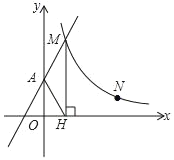
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'CD'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,则CF的长为_____.
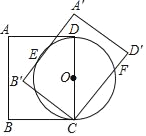
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com