
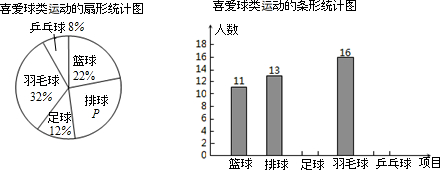
分析 (1)用1减去其它组所占的百分比即可求得p的值,根据喜欢篮球的人数是11人,所占的百分比是22%即可求得抽查的总人数,然后根据百分比的意义求得喜欢足球和乒乓球的人数,补全直方图;
(2)根据直方图即可直接确定;
(3)利用总人数乘以对应的百分比即可求解.
解答 解:(1)喜欢排球的所占的百分比p=1-22%-8%-32%-12%=26%,调查的总人数是:11÷22%=50(人),
喜欢足球的人数是50×12%=6(人),喜欢乒乓球的人数是:50×26%=13(人).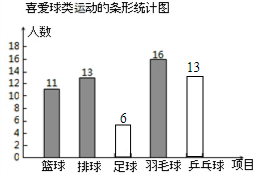 ;
;
(2)愿意参加羽毛球球类项目的人数最多;
(3)该校喜欢参加篮球和足球项目的学生共有3000×(22%+12%)=1020(人).
点评 本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
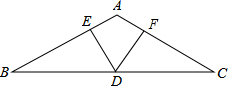 如图,在△ABC中,AB=AC,D是BC边上的点,DE⊥AB,DF⊥AC,垂足分别为E,F,∠BAC=120°,BC=12,求DE+DF的值.
如图,在△ABC中,AB=AC,D是BC边上的点,DE⊥AB,DF⊥AC,垂足分别为E,F,∠BAC=120°,BC=12,求DE+DF的值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
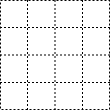 在4×4的方格中,△ABC的三个顶点均在格点上,其中AB=$\sqrt{5}$,BC=2$\sqrt{2}$,AC=$\sqrt{17}$.则△ABC中AC边上的高的长为$\frac{6\sqrt{17}}{17}$.(保留根号)
在4×4的方格中,△ABC的三个顶点均在格点上,其中AB=$\sqrt{5}$,BC=2$\sqrt{2}$,AC=$\sqrt{17}$.则△ABC中AC边上的高的长为$\frac{6\sqrt{17}}{17}$.(保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在函数y=$\frac{8}{x}$(x>0)的图象上有点P1、P2、P3…、Pn、Pn+1,点P1的横坐标
如图,在函数y=$\frac{8}{x}$(x>0)的图象上有点P1、P2、P3…、Pn、Pn+1,点P1的横坐标查看答案和解析>>
科目:初中数学 来源: 题型:解答题
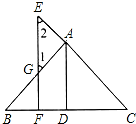 已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com