
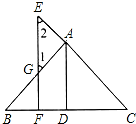
 已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.分析 根据平行线的判定推出AD∥EF,根据平行线的性质得出∠BAD=∠1,∠CAD=∠2,推出∠BAD=∠CAD即可.
解答 证明:∵AD⊥BC,EF⊥BC(已知),
∴AD∥EF(垂直于同一直线的两直线平行),
∴∠BAD=∠1(两直线平行,内错角相等),
∠CAD=∠2(两直线平行,同位角相等),
∵∠1=∠2,
∴∠BAD=∠CAD,
即AD平分∠BAC(角平分线定义),
故答案为:AD,EF,垂直于同一条直线的两条直线平行,∠BAD,∠1,∠CAD,∠2,∠1=∠2,∠BAD=∠CAD,角平分线定义.
点评 本题考查了角平分线定义,平行线的性质和判定的应用,能灵活运用平行线的性质和判定定理进行推理是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
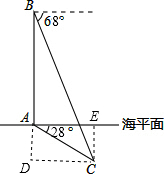 在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为27°,测得AC的距离为625米.位于军舰A正上方的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出:
在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为27°,测得AC的距离为625米.位于军舰A正上方的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=2 | B. | m≥2 | C. | m<2 | D. | m≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
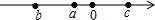 已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{{(a-c)}^2}}+\sqrt{{{(b-a)}^2}}$=c-b.
已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{{(a-c)}^2}}+\sqrt{{{(b-a)}^2}}$=c-b.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com