
| A. | 3或-1 | B. | 3 | C. | 1 | D. | -3或1 |
分析 由方程的系数结合根的判别式即可得出关于m的一元一次不等式,解之即可得出m的取值范围,再根据根与系数的关系结合$\frac{1}{α}$+$\frac{1}{β}$=-1即可得出关于m的分式方程,经检验后即可得出结论.
解答 解:∵方程x2+(2m+3)x+m2=0的两个不相等的实数根,
∴△=(2m+3)2-4m2=12m+9>0,
∴m>-$\frac{3}{4}$.
∵α,β是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根,
∴α+β=-2m-3,α•β=m2.
∵$\frac{1}{α}$+$\frac{1}{β}$=$\frac{α+β}{α•β}$=-$\frac{2m+3}{{m}^{2}}$=-1,
∴m2-2m-3=(m-3)(m+1)=1,
解得:m=3或m=-1(舍去),
经检验可知:m=3是分式方程-$\frac{2m+3}{{m}^{2}}$=-1的解.
故选B.
点评 本题考查了根的判别式以及根与系数的关系,根据根与系数的关系结合$\frac{1}{α}$+$\frac{1}{β}$=-1找出关于m的分式方程是解题的关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:解答题
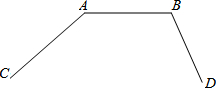 如图,已知三段公路(线段AB,以及射线AC、BD),请在AB的下方区域用尺规作一点P,使P点到三条公路的距离相等(保留作图痕迹,不写作法).
如图,已知三段公路(线段AB,以及射线AC、BD),请在AB的下方区域用尺规作一点P,使P点到三条公路的距离相等(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
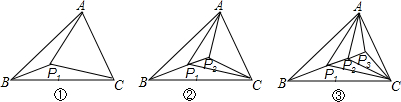
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
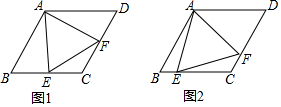
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com