
分析 化简分式可得原式=-$\frac{1}{x(x-1)}$,解方程得x=-2或x=3,将其代入代入计算可得.
解答 解:($\frac{x-1}{{x}^{2}-x}$-$\frac{x}{{x}^{2}-2x+1}$)÷$\frac{1}{x-1}$,
=[$\frac{x-1}{x(x-1)}$-$\frac{x}{(x-1)^{2}}$](x-1),
=($\frac{1}{x}$-$\frac{x}{(x-1)^{2}}$](x-1),
=-$\frac{1}{x(x-1)}$,
由x2-x-6=0,得
(x-3)(x+2)=0,
则x=3或x=-2.
当x=3时,原式=-$\frac{1}{3×(3-1)}$=-$\frac{1}{6}$;
当x=-2时,原式=-$\frac{1}{-2(-2-1)}$=-$\frac{1}{6}$.
综上所述,原式=-$\frac{1}{6}$.
点评 本题主要考查分式的化简求值、解方程的能力,熟练掌握分式的混合运算的顺序和法则及解方程的方法是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
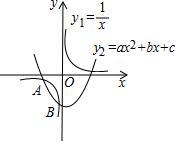 如图,反比例函数y1=$\frac{1}{x}$与二次函数y1=ax2+bx+c图象相交于A、B、C三个点,则函数y=ax2+bx-$\frac{1}{x}$+c的图象与x轴交点的个数是( )
如图,反比例函数y1=$\frac{1}{x}$与二次函数y1=ax2+bx+c图象相交于A、B、C三个点,则函数y=ax2+bx-$\frac{1}{x}$+c的图象与x轴交点的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的四个顶点在坐标轴上,点A的坐标为(-3,0),假设有甲,乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按顺时针方向匀速运动,物体乙按逆时针方向匀速运动,若物体甲12秒钟可环绕一周回到点A,物体乙24秒钟可环绕一周回到点A,则两个物体运动后的第2017次相遇地点的坐标是(1,-2).
如图,正方形ABCD的四个顶点在坐标轴上,点A的坐标为(-3,0),假设有甲,乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按顺时针方向匀速运动,物体乙按逆时针方向匀速运动,若物体甲12秒钟可环绕一周回到点A,物体乙24秒钟可环绕一周回到点A,则两个物体运动后的第2017次相遇地点的坐标是(1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 本市新建一座圆形人工湖,为测量该湖的半径,小杰和小丽沿湖边选取A,B,C三根木柱,使得A,B之间的距离与A,C之间的距离相等,并测得BC长为120米,A到BC的距离为4米,如图所示.
本市新建一座圆形人工湖,为测量该湖的半径,小杰和小丽沿湖边选取A,B,C三根木柱,使得A,B之间的距离与A,C之间的距离相等,并测得BC长为120米,A到BC的距离为4米,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com