
����Ŀ������DEF�У�DE��DF����B��EF���ϣ��ҡ�EBD��60�㣬C������BD�ϵ�һ������(�����B�غϣ���BC��BE)��������BE�Ͻ�ȡBA��BC������AC��

��1������C���߶�BD��ʱ��
������C���D�غϣ���������ⲹȫͼ1����ֱ��д���߶�AE��BF��������ϵΪ________��
����ͼ2������C�����D�غϣ���֤��AE��BF��CD��
��2������C���߶�BD���ӳ�����ʱ���õ�ʽ��ʾ�߶�AE��BF��CD֮���������ϵ������֤����
���𰸡���1����ͼ����������֤������������2��AE��BF��CD����AE��CD��BF.��
��������
����
��1������Ҫ��ȫͼ����ͼ3������֪������֤��ABD�ǵȱ������Σ���֤��DBE�ա�DAF���ɵ�BE=AF���Ӷ��ɵ�AE=BF������ͼ2����BE�Ͻ�ȡBG��BD������DG����֤��GBD����ABC���ǵȱ������Σ���֤��DGE�ա�DBF���ɵõ����������
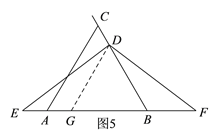
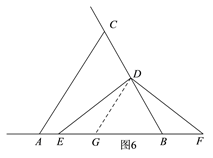
��2����ͼ5��ͼ6������C��BD�ӳ�����ʱ����ֵ�A���߶�BE�Ϻ��߶�BE���ӳ�������������������ۣ�����֪������֤��CAB�͡�DGB���ǵȱ������Σ��ɴ���DC=AG����֤��DGE�ա�DBF�ɵ�DG=BF�����ɵõ�DC��AE��BF���������ϵ.
��1������ȫͼ����ͼ3��ʾ��
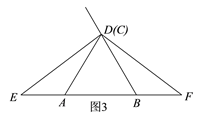
��BA=BC����EBD=60�㣬
���ABDΪ�ȱ���������
���DAB=��DBA=60�㣬DB=DA��
��DE=DF��
���E=��F��
���DBE�ա�DAF��
��BE=AF��
��BE-AB=AF-AB����AE��BF��
����ͼ4����BE�Ͻ�ȡBG��BD������DG
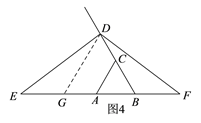
�ߡ�EBD��60�㣬BG��BD��
���GBD�ǵȱ������Σ�
ͬ������ABCҲ�ǵȱ������Σ�
��AG��CD.��DE��DF��
���E����F.
�֡ߡ�DGB����DBG��60�㣬
���DGE����DBF��120��.
���DGE�ա�DBF��
��GE��BF��
��AE��BF��CD.
��2����ͼ5��ͼ6������C��BD�ӳ�����ʱ����ֵ�A���߶�BE�Ϻ��߶�BE���ӳ�������������������ۣ�
������A���߶�BE��ʱ�����߶�BE�Ͻ�ȡBG=BD������DG��
�ߡ�DBE=60�㣬BA=BC��BG=BD��
���CBA����DBG���ǵȱ���������BA-BG=BC-BD��
���DGB=��DBG=60�㣬AG=CD��
���DGE=��DBF��
��DE=DF��
���E=��F��
���DGE�ա�DBF��
��GE=BF��
��AE=GE-AG=BF-CD��
��ͬ������ͼ6���ɵ�AE=CD-BF��
��������������C���߶�BD���ӳ�����ʱ��AE��BF��CD����AE��CD��BF��.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P��������y=x2��4x+3�ϵ�һ�㣬�Ե�PΪԲ�ġ�1����λ����Ϊ�뾶����P������P��ֱ��y=0����ʱ����P������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Rt��ABC�У���A=45������BD��CE���ڵ�ֱ�߽��ڵ�H������ͼ�β������BHC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����ȫ��ѧ����������д��������ÿλѧ����д����39���������ȡ�˲���ѧ������д��������Ƴ����µ�ͳ��ͼ������1��ͼ8.1��ͼ8.2����

����������Ϣ����������⣺
��1��ͳ�Ʊ��е�m= ��n= ��
��2����ȫ����ͳ��ͼ��
��3������ͳ��ͼ�С�E��������Ӧ��Բ�Ľ��� ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB��DE��AC��DF��AC=DF�����������������ж���ABC�ա�DEF������������

A. AB=DE B. ��B=��E C. EF=BC D. EF��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������������װ�лơ��ס��ڸ�һ�������dz�����ɫ֮��û����������
��1�������������ȡ��1������ȡ������ĸ����Ƕ��٣�
��2�������������ȡ��1���Żؽ�����ȡ�ڶ����������û���״ͼ���б��ķ�����ʾ�����п��ܳ��ֵĽ������������ȡ���Ķ��ǰ�ɫ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣮ֱ��y=kx+b��������y=mx2�� ![]() x+nͬʱ����A��0��3����B��4��0����
x+nͬʱ����A��0��3����B��4��0����
��1����m��n��ֵ��
��2����M�Ƕ��κ���ͼ����һ�㣬����M��AB�·�������M��MN��x�ᣬ��AB���ڵ�N����x�ύ�ڵ�Q����MN�����ֵ��
��3���ڣ�2���������£��Ƿ���ڵ�N��ʹ��AOB�͡�NOQ���ƣ������ڣ����N�����꣬�����ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����
��1���Ķ����⣺
���ǰ�����ij�����������е�����ɵ�ͼ�Σ�����������������ĵ�Ĺ켣��
���磺�ǵ�ƽ�����ǵ��ǵ����߾�����ȵĵ�Ĺ켣��
���⣺��ͼ1����֪EFΪ��ABC����λ�ߣ�M�DZ�BC��һ���㣬����AM��EF�ڵ�P����ô����PΪ�߶�AM�е㣮
���ɣ����߶�EFΪ��ABC����λ�ߣ���EF��BC��
��ƽ���߷��߶γɱ����ã�����PΪ�߶�AM�е㣮
�ɴ���õ�����P���˶��켣�ǣ� ��
��2��֪ʶӦ�ã�
��ͼ2����֪EFΪ�ȱߡ�ABC��AB��AC�ϵĶ��㣬����EF����AF=BE���ҵȱߡ�ABC�ı߳�Ϊ8�����߶�EF�е�Q���˶��켣�ij���
��3����չ��ߣ�
��ͼ3��PΪ�߶�AB��һ���㣨��P�����A��B�غϣ������߶�AB��ͬ��ֱ����ȱߡ�APC�͵ȱߡ�PBD������AD��BC������ΪQ��
�����AQB�Ķ�����
����AB=6����Q�˶��켣�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com