
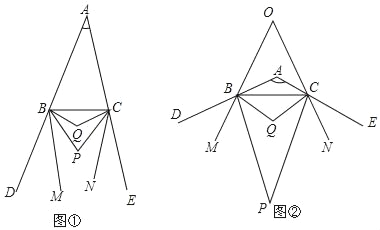
【题目】已知:如图①,BP、CP分别平分△ABC的外角∠CBD、∠BCE,BQ、CQ分别平分∠PBC、∠PCB,BM、CN分别是∠PBD、∠PCE的角平分线.
(1)当∠BAC=40°时,∠BPC= ,∠BQC= ;
(2)当BM∥CN时,求∠BAC的度数;
(3)如图②,当∠BAC=120°时,BM、CN所在直线交于点O,直接写出∠BOC的度数.
【答案】(1) 70°,125°;(2) ∠BAC=60° (3) 45°
【解析】
(1)根据三角形的外角性质分别表示出∠DBC与∠BCE,再根据角平分线的性质可求得∠CBP+∠BCP,最后根据三角形内角和定理即可求解;根据角平分线的定义得出∠QBC=![]() ∠PBC,∠QCB=
∠PBC,∠QCB=![]() ∠PCB,求出∠QBC+∠QCB的度数,根据三角形内角和定理求出即可;
∠PCB,求出∠QBC+∠QCB的度数,根据三角形内角和定理求出即可;
(2)根据平行线的性质得到∠MBC+∠NCB=180°,依此求解即可;
(3)根据题意得到∠MBC+∠NCB,再根据三角形外角的性质和三角形内角和定理得到∠BOC的度数.
(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,
∴∠CBP+∠BCP=![]() (∠DBC+∠BCE)=110°,
(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分别是∠PBC、∠PCB的角平分线,
∴∠QBC=![]() ∠PBC,∠QCB=
∠PBC,∠QCB=![]() ∠PCB,
∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分别是∠PBD、∠PCE的角平分线,
∴![]() (∠DBC+∠BCE)=180°,
(∠DBC+∠BCE)=180°,
即![]() (180°+∠BAC)=180°,
(180°+∠BAC)=180°,
解得∠BAC=60°;
(3)∵∠BAC=120°,
∴∠MBC+∠NCB=![]() (∠DBC+∠BCE)=
(∠DBC+∠BCE)=![]() (180°+α)=225°,
(180°+α)=225°,
∴∠BOC=225°﹣180°=45°.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】宜宾是国家级历史文化名城,大观楼是标志性建筑之一(如图①).喜爱数学实践活动的小伟查资料得知:大观楼始建于明代(一说是唐代韦皋所建),后毁于兵火,乾隆乙酉年(1765年)重建,它是我国目前现存最高大、最古老的楼阁之一.小伟决定用自己所学习的知识测量大观楼的高度.如图②,他利用测角仪站在B处测得大观楼最高点P的仰角为45°,又前进了12米到达A处,在A处测得P的仰角为60°.请你帮助小伟算算大观楼的高度.(测角仪高度忽略不计, ![]() ≈1.7,结果保留整数).
≈1.7,结果保留整数).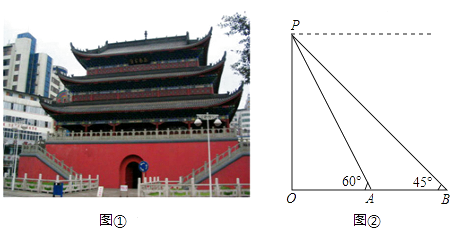
查看答案和解析>>
科目:初中数学 来源: 题型:
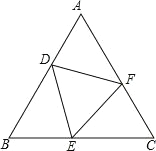
【题目】如图,△ABC 中,AB=AC,D、E、F 分别为 AB、BC、AC 上的点,且BD=CE,∠DEF=∠B.
(1)求证:∠BDE=∠CEF;
(2)当∠A=60°时,求证:△DEF 为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )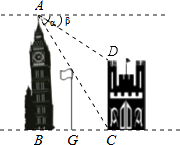
A.20米
B.10 ![]() 米
米
C.15 ![]() 米
米
D.5 ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900,且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。
(1)求证;△AOC≌△CEB
(2)求△ABD的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )
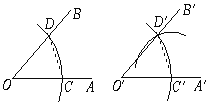
A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在图①中的正方形中剪去一个边长为2a+b的正方形,将剩余的部分按图②的方式拼成一个长方形.
(1)求剪去正方形的面积;
(2)求拼成的长方形的长、宽以及它的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( ) 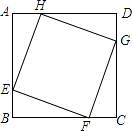
A.30
B.34
C.36
D.40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com