
����Ŀ���˱��ǹ��Ҽ���ʷ�Ļ����ǣ����¥�DZ�־�Խ���֮һ����ͼ�٣���ϲ����ѧʵ�����Сΰ�����ϵ�֪�����¥ʼ����������һ˵���ƴ�Τ��������������ڱ���Ǭ¡�����꣨1765�꣩�ؽ��������ҹ�Ŀǰ�ִ���ߴ�����ϵ�¥��֮һ��Сΰ�������Լ���ѧϰ��֪ʶ�������¥�ĸ߶ȣ���ͼ�ڣ������ò����վ��B����ô��¥��ߵ�P������Ϊ45�㣬��ǰ����12����A������A�����P������Ϊ60�㣮�������Сΰ������¥�ĸ߶ȣ�������Ǹ߶Ⱥ��Բ��ƣ� ![]() ��1.7�����������������
��1.7�����������������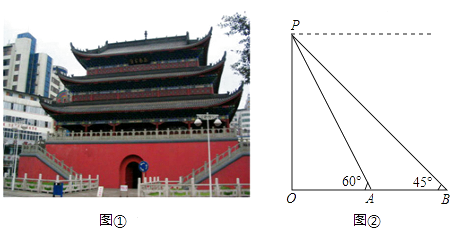
 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���B��65�㣬��BAD��40�㣬��AED��100�㣬��CDE��45�㣬���CAD�Ķ�����
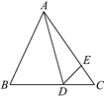
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪���� DM��ֱ��AB���ڵ�A���߶�EC��ֱ��AB���ڵ�C��AB��DE.
(1)����MAC��100�㣬��BCE��120��ʱ����EC�Ƶ�E��ת���Ƕ�(����Ƕ�С��180��)ʱ�����ж�MD��EC��������Ƴ����ַ�������������ͼ��
(2)����EC�Ƶ�E��ʱ����ת60��ʱ����C���Aǡ���غϣ��뻭����ͼ������ͼ���ҳ�ͬλ�ǡ��ڴ��Ǹ�����(�������ֱ���ǣ��ٻش�)��
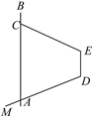
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ͼ1���ڡ�ABC�͡�ADE�У�AB=AC=AD=AE������BAC+��DAE=180�� ʱ�����dzơ�ABC���DAE��Ϊ���������������Ρ�����ABC�ı�BC�ϵĸ���AM������ADE�ġ����ľࡱ����A�������������ġ�.

��1��������֪����ͼ2��ͼ3�У���ABC���DAE��Ϊ���������������Ρ���AM�ǡ����ľࡱ��
����ͼ2������BAC=90��ʱ��AM��DE֮���������ϵΪAM=�� ��DE��
����ͼ3������BAC=120�㣬ED=6ʱ��AM�ij�Ϊ�� ����
��2��������֤��
��ͼ1�У�����BACΪ�����ʱ������AM��DE֮���������ϵ��������֤����

��3����չӦ��
��ͼ4�����ı���ABCD�У�AD=AB��CD=BC����B=90�㣬��A=60�㣬CA=![]() �����ı�ABCD���ڲ��ҵ���P��ʹ�á�PAD���PBC��Ϊ���������������Ρ������ش�����������
�����ı�ABCD���ڲ��ҵ���P��ʹ�á�PAD���PBC��Ϊ���������������Ρ������ش�����������
������ͼ�б����P��λ�ã����������õ��λ��Ϊ ��
��ֱ��д����PBC�ġ����ľࡱ�ij�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2013��4��20�գ���ʡ«ɽ�ط���7.0��ǿ�ҵ�����ɴ����ķ�����٣������������ij��ҵ�ӵ��������ڹ涨ʱ��������һ�����������ԭ���������ٶȣ�ÿ������120��������ô�ڹ涨ʱ����ֻ����������90%��Ϊ��ʱ���������ҵ������Ա��֧Ԯ��������һ�ߣ�������ÿ��������160�����պ���ǰһ����������ʹ涨ʱ���Ƕ����죿���������Ƕ��ٶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1��ʼ��������Ȼ����ͼ�������У��涨λ�ڵ�3�У���2�е���Ȼ��10��Ϊ��3��2������Ȼ��15��Ϊ��4��2��������
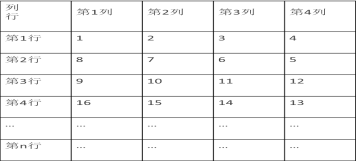
���˹��ɣ��ش��������⣺
��1����Ϊ��6��3����ʾ����Ȼ����___________��
��2����Ȼ��2018��Ϊ __________��
��3����һ�������η����ڵ�3�к͵�4����������ĸ��������ĸ����ĺ���Ϊ2018������ܣ����������ĸ�������С������������ܣ���д�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ֲ�ͬ�ķ�������ͬһͼ�ε����ʱ�����Եõ�һ����ʽ�����磬��ͼ�٣��ɵõ�ʽ��(a��2b)(a��b)��a2��3ab��2b2.
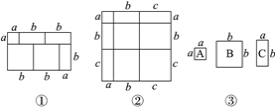
(1)��ͼ�ڣ�д�����õĵ�ʽ��
(2)����(1)�����õ��Ľ��ۣ������������⣺ ��֪a��b��c��11��ab��bc��ac��38����a2��b2��c2��ֵ��
(3)��ͼ�ۣ�������2 ��A��ֽƬ��3 ��B��ֽƬ��5 ��C��ֽƬƴ��һ�������Σ���ô�ó����νϳ���һ���߳�Ϊ���٣�(ֱ��д����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������A��ʻ��B�أ�ǰ����֮һ·��Ϊ��ͨ��·������·��Ϊ���ٹ�·����֪��������ͨ��·����ʻ���ٶ�Ϊ60km/h���ڸ��ٹ�·����ʻ���ٶ�Ϊ100km/h��������A�ص�B�ع���ʻ��2.2h���������������Ϣ����������ʻ�ġ�·�̡���ʱ�䡱�����һ�����⣺�� �������г����̣�����⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
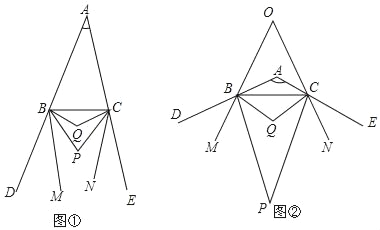
����Ŀ����֪����ͼ�٣�BP��CP�ֱ�ƽ����ABC�������CBD����BCE��BQ��CQ�ֱ�ƽ����PBC����PCB��BM��CN�ֱ�����PBD����PCE�Ľ�ƽ���ߣ�
��1������BAC=40��ʱ����BPC=�� ������BQC=�� ����
��2����BM��CNʱ������BAC�Ķ�����
��3����ͼ��������BAC=120��ʱ��BM��CN����ֱ�߽��ڵ�O��ֱ��д����BOC�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com