
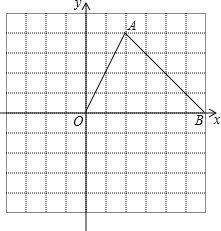
【题目】如图在平面直角坐标系中,△OAB的顶点坐标分别是O(0,0),A(2,4),B(6,0).
(1)以原点O为位似中心,在点O的异侧画出△OAB的位似图形△OA1B1,使它与△OAB的相似比是1:2.
(2)写出点A1、B1的坐标.
(3)若△OAB关于点O的位似图形△OA2B2中,点A的对应点A2的坐标为(﹣3,﹣6),则△OA2B2与△OAB的相似比为______.
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象上部分点的横坐标
图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| ··· | -3 | -2 | -1 | 0 | ··· |
| ··· | 0 | -3 | -4 | -3 | ··· |
直接写出不等式![]() 的解集是____________________.
的解集是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
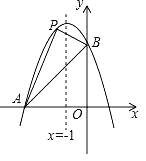
(1)求此抛物线的解析式.
(2)若点Q是对称轴上一动点,当OQ+BQ最小时,求点Q的坐标.
(3)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB面积的最大值,并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
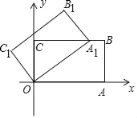
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF、BF、EF,过点F作GF⊥AF交AD于点G,设AD:AE=n.
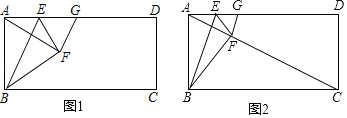
(1)线段AE和线段EG的数量关系是: ;
(2)如图②,当点F落在AC上时,用含n的代数式表示AD:AB的值;
(3)若AD=4AB,且△FCG为直角三角形,求n的值.(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中两条直线OC⊥BC,垂足为C,其OC=2cm,∠COB=60°,反比例函数y=![]() 的图象过点C.
的图象过点C.
(1)求:反比例函数表达式和点B的坐标.
(2)若现有长为1cm的线段MN在线段OB上沿OB方向以1cm/s的速度向点B运动(运动前点M与点O重合,N到点B停止运动),过M、N作OB的垂线分别交直线OC、BC于P、Q两点,线段MN运动的时间为ts.
①若△OMP的面积为S.求出当0<t≤1时,S与t的函数关系式.
②线段MN运动过程中,四边形MNQP有可能成为矩形吗?若可能,直接写出此时t的值;若不可能,说明理由.
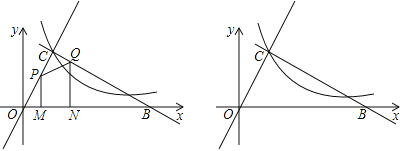
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若某抛物线上有两点A、B关于原点对称,则称该抛物线为“完美抛物线”.已知二次函数y=ax2-2mx+c(a,m,c均为常数且ac≠0)是“完美抛物线”:
(1)试判断ac的符号;
(2)若c=-1,该二次函数图象与y轴交于点C,且S△ABC=1.
①求a的值;
②当该二次函数图象与端点为M(-1,1)、N(3,4)的线段有且只有一个交点时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com