Question

【题目】定义：若某抛物线上有两点A、B关于原点对称，则称该抛物线为“完美抛物线”．已知二次函数y=ax2-2mx+c（a，m，c均为常数且ac≠0）是“完美抛物线”：

（1）试判断ac的符号；

（2）若c=-1，该二次函数图象与y轴交于点C，且S△ABC=1．

①求a的值；

②当该二次函数图象与端点为M（-1，1）、N（3，4）的线段有且只有一个交点时，求m的取值范围．

Answer 1

【答案】(1) ac＜0；(2)①a=1；②m＞或m＜．

【解析】

（1）设A（p，q）．则B（-p，-q），把A、B坐标代入解析式可得方程组即可得到结论；
（2）由c=-1，得到p2＝，a＞0，且C（0，-1），求得p＝±，①根据三角形的面积公式列方程即可得到结果；②由①可知：抛物线解析式为y=x2-2mx-1，根据M（-1，1）、N（3，4）．得到这些MN的解析式y＝x+（-1≤x≤3），联立方程组得到x2-2mx-1=x+，故问题转化为：方程x2-（2m+）x-=0在-1≤x≤3内只有一个解，建立新的二次函数：y=x2-（2m+）x-，根据题意得到（Ⅰ）若-1≤x1＜3且x2＞3，（Ⅱ）若x1＜-1且-1＜x2≤3：列方程组即可得到结论．

（1）设A（p，q）．则B（-p，-q），
把A、B坐标代入解析式可得：

，
∴2ap2+2c=0．即p2＝，
∴≥0，
∵ac≠0，
∴＞0，
∴ac＜0；
（2）∵c=-1，
∴p2＝，a＞0，且C（0，-1），
∴p＝±，
①S△ABC=×2×1=1，
∴a=1；
②由①可知：抛物线解析式为y=x2-2mx-1，
∵M（-1，1）、N（3，4）．
∴MN：y＝x+（-1≤x≤3），
依题，只需联立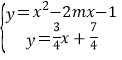在-1≤x≤3内只有一个解即可，
∴x2-2mx-1=x+，
故问题转化为：方程x2-（2m+）x-=0在-1≤x≤3内只有一个解，
建立新的二次函数：y=x2-（2m+）x-，
∵△=（2m+）2+11＞0且c=-＜0，
∴抛物线y＝x2(2m+)x与x轴有两个交点，且交y轴于负半轴．
不妨设方程x2(2m+)x＝0的两根分别为x1，x2．（x1＜x2）
则x1+x2＝2m+，x1x2＝
∵方程x2(2m+)x＝0在-1≤x≤3内只有一个解．
故分两种情况讨论：
（Ⅰ）若-1≤x1＜3且x2＞3：则

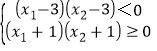．即：，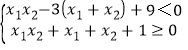
可得：m＞．
（Ⅱ）若x1＜-1且-1＜x2≤3：则

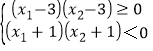．即：，
可得：m＜，
综上所述，m＞或m＜．