
【题目】如图,在长方形ABCD中,AB=5,AD=12,点E是BC上一点,将△ABE沿AE折叠,使点B落在点F处,连接CF,当△CEF为直角三角形时,CF的长为________。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】若a,b是一元二次方程x(x﹣2)=x﹣2的两根,且点A(﹣a,﹣b)是反比例函数图象上的一个点,若自点A向两坐标轴作垂线,两垂线与坐标轴构成的矩形的面积是( )
A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:甲、乙两车分别从相距300km的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离y与行驶时间x之间的函数图象.
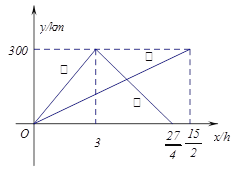
(1)求甲车离出发地的距离y与行驶时间x之间的函数关系式,并标明自变量![]() 的取值范围;
的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)它们在行驶过程中有几次相遇.并求出每次相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为CD上一点,连接BE, ∠EBC=15°,将ΔEBC绕点C按顺时针方向旋转90°得到ΔFDC,连接EF,则∠EFD的度数为( )

A. 15° B. 20° C. 25° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%.为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图,如图所示.下面有四个推断:

①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量不超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150~180m3之间;
④该市居民家庭年用水量的众数约为110m3.
其中合理的是( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若某抛物线上有两点A、B关于原点对称,则称该抛物线为“完美抛物线”.已知二次函数y=ax2-2mx+c(a,m,c均为常数且ac≠0)是“完美抛物线”:
(1)试判断ac的符号;
(2)若c=-1,该二次函数图象与y轴交于点C,且S△ABC=1.
①求a的值;
②当该二次函数图象与端点为M(-1,1)、N(3,4)的线段有且只有一个交点时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
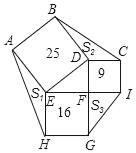
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,点A、点B在直线l异侧,以点A为圆心,AB长为半径作弧交直线l于C、D两点.分别以C、D为圆心,AB长为半径作弧,两弧在l下方交于点E,连结AE.
(1)根据题意,利用直尺和圆规补全图形;
(2)证明:l垂直平分AE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com