
ЁОЬтФПЁПвбжЊЃКМзЁЂввСНГЕЗжБ№ДгЯрОр300kmЕФA,BСНЕиЭЌЪБГіЗЂЯрЯђЖјааЃЌМзЕНBЕиКѓСЂМДЗЕЛиЃЌЯТЭМЪЧЫќУЧРыИїздГіЗЂЕиЕФОрРыyгыааЪЛЪБМфxжЎМфЕФКЏЪ§ЭМЯѓ.
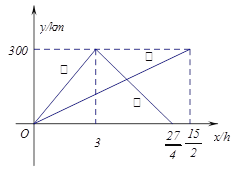
ЃЈ1ЃЉЧѓМзГЕРыГіЗЂЕиЕФОрРыyгыааЪЛЪБМфxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂБъУїздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєвбжЊввГЕааЪЛЕФЫйЖШЪЧ40ЧЇУз/аЁЪБЃЌЧѓГіЗЂКѓЖрГЄЪБМфЃЌСНГЕРыИїздГіЗЂЕиЕФОрРыЯрЕШЃЛ
ЃЈ3ЃЉЫќУЧдкааЪЛЙ§ГЬжагаМИДЮЯргі.ВЂЧѓГіУПДЮЯргіЕФЪБМф.
ЁОД№АИЁП(1) 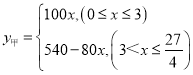 ;(2)4.5аЁЪБ;(3) :СНДЮЪзДЮЯргідк
;(2)4.5аЁЪБ;(3) :СНДЮЪзДЮЯргідк![]() h,ЕкЖўДЮЯргідк6h.
h,ЕкЖўДЮЯргідк6h.
ЁОНтЮіЁП
(1)ЩшГіНтЮіЪН,ЗжЖЮЬжТлДњжЕНтГіМДПЩ.
(2)гЩЭМЕУГіввГЕЖдгІЕФвЛДЮКЏЪ§гыМзГЕвЛДЮКЏЪ§СЊСЂНтГіРДМДПЩ.
(3)гЩЭМПЩжЊМзввгаСНДЮЯргі,ЗжБ№ЬжТлМЦЫуМДПЩ.
(1)ЕБ0ЁмxЁм3ЪБ,ЪЧе§БШР§КЏЪ§,ЩшЮЊy=kx,
ЕБx=3ЪБ,y=300,ДњШыНтЕУk=100,Ыљвдy=100xЃЛ
ЕБ3ЃМxЁм![]() ЪБ,ЪЧвЛДЮКЏЪ§,ЩшЮЊy=kx+b,
ЪБ,ЪЧвЛДЮКЏЪ§,ЩшЮЊy=kx+b,
ДњШыСНЕуЃЈ3,300ЃЉЁЂЃЈ![]() ,0ЃЉ,НтЕУk=-80,b=540,Ыљвдy=540-80x ЃЎ
,0ЃЉ,НтЕУk=-80,b=540,Ыљвдy=540-80x ЃЎ
злКЯвдЩЯЕУМзГЕРыГіЗЂЕиЕФОрРыyгыааЪЛЪБМфxжЎМфЕФКЏЪ§ЙиЯЕЪН
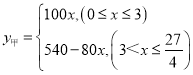
(2)гЩЬтвтЕУ:yвв=40xЃЎЃЈ0ЁмxЁм![]() ЃЉ
ЃЉ
ЕБ40x=100xЪБ,ЮоНтЩсШЅ
ЕБ40x=540-80xЪБ,НтЕУx=4.5
ГіЗЂКѓ4.5аЁЪБ,СНГЕРыИїздГіЗЂЕиЕФОрРыЯрЕШ.
(3)гЩЭМЯѓПЩЕУгаСНДЮЯргі.
ЩшОЙ§aаЁЪБСНГЕЪзДЮЯргі,дђ40a+100a=300,НтЕУa=![]() ,
,
ЩшОЙ§bаЁЪБСНГЕЕкЖўДЮЯргі,дђ80ЃЈb-3ЃЉ=40b,НтЕУb=6ЃЎ
Д№:СНДЮЪзДЮЯргідк![]() h,ЕкЖўДЮЯргідк6h.
h,ЕкЖўДЮЯргідк6h.


 ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ
ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ
вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОгаAаЭВњЦЗ40МўЃЌBаЭВњЦЗ60МўЃЌЗжХфИјЯТЪєМзЁЂввСНИіЩЬЕъЯњЪлЃЌЦфжа70МўИјМзЕъЃЌ30МўИјввЕъЃЌЧвЖМФмТєЭъ.СНЩЬЕъЯњЪлетСНжжВњЦЗУПМўЕФРћШѓЃЈдЊЃЉШчЯТБэ.ЩшЗжХфИјМзЕъAаЭВњЦЗ![]() МўЃЌетМвЙЋЫОТєГіет100МўВњЦЗЕФзмРћШѓЮЊWЃЈдЊЃЉ.
МўЃЌетМвЙЋЫОТєГіет100МўВњЦЗЕФзмРћШѓЮЊWЃЈдЊЃЉ.

ЃЈ1ЃЉЧѓWЙигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГі
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГі![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєЙЋЫОвЊЧѓзмРћШѓВЛЕЭгк17560дЊЃЌЫЕУїгаЖрЩйжжВЛЭЌЗжХфЗНАИЃП
ЃЈ3ЃЉЪЕМЪЯњЪлЙ§ГЬжаЃЌЙЋЫОЗЂЯжетХњВњЦЗгШЦфЪЧAаЭВњЦЗКмГЉЯњЃЌБуОіЖЈЖдМзЕъЕФзюКѓ21МўAаЭВњЦЗУПМўЬсМл![]() дЊЯњЪлЃЈ
дЊЯњЪлЃЈ![]() ЮЊе§ећЪ§ЃЉ.СНЕъШЋВПЯњЪлЭъБЯКѓНсЙћЕФзмРћШѓЮЊ18000дЊЃЌЧѓ
ЮЊе§ећЪ§ЃЉ.СНЕъШЋВПЯњЪлЭъБЯКѓНсЙћЕФзмРћШѓЮЊ18000дЊЃЌЧѓ![]() жЕ.ВЂаДГіЙЋЫОет100МўВњЦЗЖдМзввСНЕъЪЧШчКЮЗжХфЕФЃП
жЕ.ВЂаДГіЙЋЫОет100МўВњЦЗЖдМзввСНЕъЪЧШчКЮЗжХфЕФЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(1)НтЗНГЬЃК ![]() Ѓ2ЃН
Ѓ2ЃН![]() ЃЛ
ЃЛ
(2)ЩшyЃНkxЃЌЧвkЁй0ЃЌШєДњЪ§ЪН(xЃ3y)(2xЃЋy)ЃЋy(xЃЋ5y)ЛЏМђЕФНсЙћЮЊ2x2ЃЌЧѓkЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧЕШбќжБНЧ
ЪЧЕШбќжБНЧ![]() ЭтвЛЕуЃЌАб
ЭтвЛЕуЃЌАб![]() ШЦжБНЧЖЅЕу
ШЦжБНЧЖЅЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЕН
ЕН![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊ________ЃЎ
ЕФжЕЮЊ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬk2x2Љ2ЃЈk+1ЃЉx+1=0гаСНИіЪЕЪ§ИљЃЎ
ЃЈ1ЃЉЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБk=1ЪБЃЌЩшЫљИјЗНГЬЕФСНИіИљЗжБ№ЮЊx1КЭx2ЃЌЧѓЃЈx1Љ2ЃЉЃЈx2Љ2ЃЉЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќжБНЧЁїABCжаЃЌЁЯACB=90ЁуЃЌOЪЧаББпABЕФжаЕуЃЌЕуDЁЂEЗжБ№дкжБНЧБпACЁЂBCЩЯЃЌЧвЁЯDOE=90ЁуЃЌDEНЛOCгкЕуPЃЌдђЯТСаНсТлЃКЂйЭМжаШЋЕШЕФШ§НЧаЮжЛгаСНЖдЃЛЂкЁїABCЕФУцЛ§ЕШгкЫФБпаЮCDOEУцЛ§ЕФ2БЖЃЛЂлOD=OEЃЛЂмCE+CD=BCЃЌЦфжае§ШЗЕФНсТлгаЃЈ ЃЉ

AЃЎ1Иі BЃЎ2Иі CЃЎ3Иі DЃЎ4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() НЛ
НЛ![]() гк
гк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() дк
дк![]() ЃЌ
ЃЌ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() .
.

ЃЈ1ЃЉЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНаЮABCDжаЃЌAB=5ЃЌAD=12ЃЌЕуEЪЧBCЩЯвЛЕуЃЌНЋЁїABEбиAEелЕўЃЌЪЙЕуBТфдкЕуFДІЃЌСЌНгCFЃЌЕБЁїCEFЮЊжБНЧШ§НЧаЮЪБЃЌCFЕФГЄЮЊ________ЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋвЛИіжБНЧШ§НЧаЮжНЦЌABOЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЈ![]() ЃЌ0ЃЉЃЌBЃЈ0ЃЌ1ЃЉЃЌOЃЈ0ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЌBЃЈ0ЃЌ1ЃЉЃЌOЃЈ0ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЕуPЮЊБпOAЩЯвЛЕуЃЈЕуPВЛгыAЃЌOжиКЯЃЉЃЌбиBPНЋжНЦЌелЕўЕУAЕФЖдгІЕуAЁфЃЎБпBAЁфгыxжсНЛгкЕуQЃЎ
ЂйШчЭМ1ЃЌЕБЕуAЁфИеКУТфдкyжсЩЯЪБЃЌЧѓЕуAЁфЕФзјБъЃЎ
ЂкШчЭМ2ЃЌЕБAЁфPЁЭOAЃЌШєЯпЖЮOQдкxжсЩЯвЦЖЏЕУЕНЯпЖЮOЁфQЁфЃЈЯпЖЮOQЦНвЦЪБAЁфВЛЖЏЃЉЃЌЕБЁїAЁфOЁфQЁфжмГЄзюаЁЪБЃЌЧѓOOЁфЕФГЄЖШЃЎ
ЃЈ2ЃЉШчЭМ3ЃЌШєЕуPЮЊБпABЩЯвЛЕуЃЈЕуPВЛгыAЃЌBжиКЯЃЉЃЌбиOPНЋжНЦЌелЕўЕУAЕФЖдгІЕуAЁхЃЌЕБЁЯBPAЁхЃН30ЁуЪБЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com