
【题目】将一个直角三角形纸片ABO放置在平面直角坐标系中,点A(![]() ,0),B(0,1),O(0,0).
,0),B(0,1),O(0,0).
(1)点P为边OA上一点(点P不与A,O重合),沿BP将纸片折叠得A的对应点A′.边BA′与x轴交于点Q.
①如图1,当点A′刚好落在y轴上时,求点A′的坐标.
②如图2,当A′P⊥OA,若线段OQ在x轴上移动得到线段O′Q′(线段OQ平移时A′不动),当△A′O′Q′周长最小时,求OO′的长度.
(2)如图3,若点P为边AB上一点(点P不与A,B重合),沿OP将纸片折叠得A的对应点A″,当∠BPA″=30°时,求点P的坐标.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:甲、乙两车分别从相距300km的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离y与行驶时间x之间的函数图象.
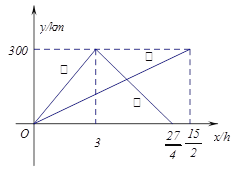
(1)求甲车离出发地的距离y与行驶时间x之间的函数关系式,并标明自变量![]() 的取值范围;
的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)它们在行驶过程中有几次相遇.并求出每次相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
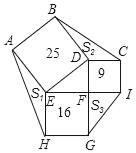
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为![]() 和
和![]() ,将菱形的“接近度”定义为
,将菱形的“接近度”定义为![]() ,于是,
,于是,![]() 越小,菱形越接近于正方形.
越小,菱形越接近于正方形.
①若菱形的一个内角为![]() ,则该菱形的“接近度”等于 ;
,则该菱形的“接近度”等于 ;
②当菱形的“接近度”等于 时,菱形是正方形.

(2)设矩形相邻两条边长分别是![]() 和
和![]() (
(![]() ),将矩形的“接近度”定义为
),将矩形的“接近度”定义为![]() ,于是
,于是![]() 越小,矩形越接近于正方形.
越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=1,则△A8B8A9的边长_________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
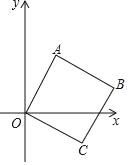
A. (![]() ,-1) B. (2,﹣1) C. (1,-
,-1) B. (2,﹣1) C. (1,-![]() ) D. (﹣1,
) D. (﹣1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,点A、点B在直线l异侧,以点A为圆心,AB长为半径作弧交直线l于C、D两点.分别以C、D为圆心,AB长为半径作弧,两弧在l下方交于点E,连结AE.
(1)根据题意,利用直尺和圆规补全图形;
(2)证明:l垂直平分AE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=120°,AD平分∠BAC,且AD=AB,若∠EDF=60°,其两边分别交边AB,AC于点E,F.
(1)求证:△ABD是等边三角形;
(2)求证:BE=AF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com