
【题目】在△ABC中,∠BAC=120°,AD平分∠BAC,且AD=AB,若∠EDF=60°,其两边分别交边AB,AC于点E,F.
(1)求证:△ABD是等边三角形;
(2)求证:BE=AF.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接BD,根据角平分线的性质可得∠BAD=60°,又因为AD=AB,即可证△ABD是等边三角形;(2)由△ABD是等边三角形,得出BD=AD,∠ABD=∠ADB=60°,证出∠BDE=∠ADF,由ASA证明△BDE≌△ADF,得出BE=AF.
(1)证明:连接BD,
∵∠BAC=120°,AD平分∠BAC
∴∠BAD=∠DAC=![]() ×120°=60°,
×120°=60°,
∵AD=AB,
∴△ABD是等边三角形;
(2)证明:∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BD=AD,
∵∠DAC=![]() ∠BAC=60°,
∠BAC=60°,
∴∠DBE=∠DAF,
∵∠EDF=60°,
∴∠BDE=∠ADF,
在△BDE与△ADF中,
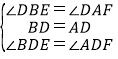 ,
,
∴△BDE≌△ADF(ASA),
∴BE=AF.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=2 ![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 .
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 . 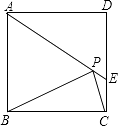
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某超市购买A、B、C三种商品.其中A、B两种商品的单价之和正好等于C商品的单价,小明前两次购买商品的数量和总费用如下表:
商品A的数量 | 商品B的数量 | 商品C的数量 | 总费用(元) | |
第一次 | 2 | 3 | 2 | 230 |
第二次 | 1 | 4 | 3 | 290 |
(1)求A、B、C三种商品的单价;
(2)若小明第三次需要购置A、B、C三种商品共m个,其中C商品的数量是A商品的数量的2倍,恰好花了480元钱.
①求m的最大值;
②若小明在第三次购买A,B,C三种商品时正好遇上“买一送一”活动,即购买一个C商品即可赠送一个A商品或一个B商品(优先赠送A商品),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
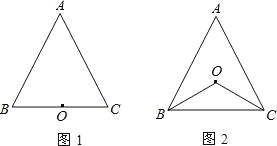
(1)如图1,若点O在BC上,求证:△ABC是等腰三角形.
(2)如图2,若点O在△ABC内部,求证:AB=AC.
(3)若点O点在△ABC的外部,△ABC是等腰三角形还成立吗?请画图表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,家电商场进行促销活动,有两种促销方式,方式一:出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物:方式二:若不买卡,则打9.5折销售
(1)买一台标价为3500的冰箱,方式一应付_____元,方式二应付_____元.
(2)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?如何购物合算?(只需给出结论,不用写计算过程)
(3)小张按合算的方案把这台冰箱买下,如果家电商场还能盈利 25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
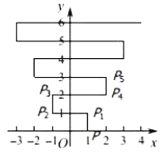
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() .点
.点![]() 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点![]() ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点![]() ,第3次向上跳动1个单位至点
,第3次向上跳动1个单位至点![]() ,第4次向右跳动3个单位至点
,第4次向右跳动3个单位至点![]() ,第5次又向上跳动1个单位至点
,第5次又向上跳动1个单位至点![]() ,第6次向左跳动4个单位至点
,第6次向左跳动4个单位至点![]() ,……,照此规律,点
,……,照此规律,点![]() 第2020次跳动至点
第2020次跳动至点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com