
����Ŀ�����ڣ��ҵ��̳����д�����������ִ�����ʽ����ʽһ������һ���Żݹ��│(ע���˿�ֻ��Ϊ�����Ż�ƾ֤���ܶ������)����300Ԫ�����ֿ���ƾ����������̳�����۵�8�۹����ʽ�������������9.5������
(1)��һ̨���Ϊ3500�ı��䣬��ʽһӦ��_____Ԫ����ʽ��Ӧ��_____Ԫ��
(2)�˿������Ԫ������Ʒʱ�����벻��Ǯ���?��ι������?(ֻ��������ۣ�����д�������)
(3)С�Ű�����ķ�������̨�������£�����ҵ��̳�����ӯ�� 25%����̨����Ľ����Ƕ���Ԫ?
���𰸡���1��3100��3325 ��2��2000���˿���С��2000Ԫ������Ʒʱ������Ǯ���㣻�˿���2000Ԫ������Ʒʱ�����벻��Ǯ��ȣ��˿������2000Ԫ������Ʒʱ����Ǯ���㣮 ��3��2480
��������
��1����������������ַ�ʽ�Ļ��Ѽ��ɣ�
��2���˿���xԪ������Ʒʱ�����벻��Ǯ��ȣ����������г�������⣬�ٷ�����ж���ι�����㣮
��3����ϣ�1���ɵ�С�������Ļ��ѣ�����![]() �����������̨����Ľ��ۣ�
�����������̨����Ľ��ۣ�
��1����ʽһ��![]() ��Ԫ��
��Ԫ��
��ʽ����![]() ��Ԫ��
��Ԫ��
����һ̨���Ϊ3500�ı��䣬��ʽһӦ��3100Ԫ����ʽ��Ӧ��3325Ԫ��
��2���˿���xԪ������Ʒʱ�����벻��Ǯ���
![]()
���![]()
�ʹ˿���2000Ԫ������Ʒʱ�����벻��Ǯ���
�ɴ˿ɵã��˿������2000Ԫ������Ʒʱ����Ǯ���ۿ����ȸ���
�ʹ˿���С��2000Ԫ������Ʒʱ������Ǯ���㣻
�˿���2000Ԫ������Ʒʱ�����벻��Ǯ��ȣ�
�˿������2000Ԫ������Ʒʱ����Ǯ���㣮
��3���ɣ�1���ã�����˱��䷽ʽһ������
![]() ��Ԫ��
��Ԫ��
����̨����Ľ�����2480Ԫ��


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD=��CAE=90�㣬AB=AD��AE=AC��AF��CB������ΪF��
��1����֤����ABC�ա�ADE����ͼ1��
��2�����FAE�Ķ�������ͼ1��
��3����ͼ2���ӳ�CF��G�㣬ʹBF=GF������AG����֤��CD=CG��������CD��2BF+DE�Ĺ�ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���BAC��120�㣬ADƽ�֡�BAC����AD��AB������EDF��60���������߷ֱ�AB��AC�ڵ�E��F��
��1����֤����ABD�ǵȱ������Σ�
��2����֤��BE��AF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ֱ�����dzߣ���ֱ��������AOB��ֱ��������COD����ֱ�Ƕ���O���غϣ����У�����AOB�У���A=60������B=30������AOB=90��������COD�У���C=��D=45������COD=90����
��1����ͼ1����OA�ڡ�COD���ⲿ���ҡ�AOC=45��ʱ������˵��COƽ�֡�AOB�� ����˵��OA��CD��Ҫ����д���̣���
��2����ͼ2���Ƶ�O��תֱ�����dz�AOB��ʹOA�ڡ�COD���ڲ�����CD��OB����̽����AOC=45���Ƿ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
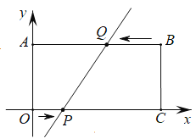
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�ı�OC��OA�ֱ���x�ᡢy���ϣ�B���ڵ�һ���ޣ���A�������ǣ�0��4����OC=8��
��1��ֱ��д����B��C�����ꣻ
��2����P��ԭ��O�������ڱ�OC����ÿ��1����λ���ȵ��ٶ�������C���ƶ���ͬʱ��Q�ӵ�B�������ڱ�BA����ÿ��2����λ���ȵ��ٶ�������A���ƶ�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�ƶ������ƶ���ʱ��Ϊt���ӣ�̽���������⣺
�� ��tֵΪ����ʱ��ֱ��PQ��y�
�� �������˶������У��ܷ�ʹ���ı���BCPQ������dz�����OABC�������![]() �����ܣ���ֱ��д��P��Q��������ꣻ�����ܣ�˵��������
�����ܣ���ֱ��д��P��Q��������ꣻ�����ܣ�˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�����Ϊ84��BC��21���ֽ���ABC��ֱ��BC����ƽ��a��0��a��21������λ����DEF��λ�ã�
��1����BC���ϵĸߣ�
��2����AB��10��
�����߶�DF�ij���
������AE������ABEʱ����������ʱ����a��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y=x2��2mx��3�����н��۴�����ǣ� ��
A.����ͼ����x������������
B.����x2��2mx=3������֮��Ϊ��3
C.����ͼ��ĶԳ�����y����Ҳ�
D.x��mʱ��y��x���������С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ͼ2�У���CΪ�߶�AB��һ�㣬��ACM����CBN���ǵȱ�������.
(1) ��ͼ1���߶�AN���߶�BM�Ƿ���ȣ�֤����Ľ��ۣ�
(2) ��ͼ2��AN��MC���ڵ�E��BM��CN���ڵ�F��̽����CEF����״����֤����Ľ���.

ͼ1 ͼ2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com