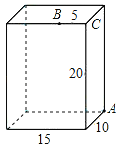
【题目】如图，一个放置在地面上的长方体，长为15cm，宽为10cm，高为20cm，点B与点C的距离为5cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是多少？
【答案】需要爬行的最短距离是25cm．
【解析】
要求长方体中两点之间的最短路径，最直接的作法，就是将长方体侧面展开，然后利用两点之间线段最短解答．
（1）把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形，如图1．
∵长方体的宽为10，高为20，点B离点C的距离是5，
∴BD=CD+BC=10+5=15，AD=20，
在直角三角形ABD中，根据勾股定理得：
AB
（cm）；
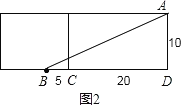
（2）把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形，如图2．
∵长方体的宽为10，高为20，点B离点C的距离是5，
∴BD=CD+BC=20+5=25，AD=10，
在直角三角形ABD中，根据勾股定理得：
AB
（cm）；
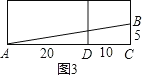
（3）把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形，如图3．
∵长方体的宽为10，高为20，点B离点C的距离是5，
∴AC=CD+AD=20+10=30，
在直角三角形ABC中，根据勾股定理得：
AB
（cm）．
∵25＜5
，∴蚂蚁爬行的最短距离是25cm．
答：需要爬行的最短距离是25cm．
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，点A(2，0)，点B (0，1)，过点A的直线l垂直于线段AB，点P是直线l上一动点，过点P作PC⊥x轴，垂足为C，把△ACP沿AP翻折
，使点C落在点D处，若以A，D，P为顶点的三角形与△ABP相似，则所有满足此条件的点P的坐标为___________________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场将进货价为30元的台灯以40元的价格售出，平均每月能售出600个，经调查表明，这种台灯的售价每上涨1元，其销量就减少10个，市场规定此台灯售价不得超过60元，为了实现销售这种台灯平均每月10000元的销售利润，售价应定为多少元？这时售出台灯多少个？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，AC平分∠DAB，AC2=ABAD，∠ADC=90°，E为AB的中点．
（1）求证：△ADC∽△ACB；
（2）CE与AD有怎样的位置关系？试说明理由；
（3）若AD=4，AB=6，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．
下面有三个推断：
①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；
②随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；
③若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率一定是0.620．
其中合理的是（ ）
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB＝AC，AM是△ABC的外角∠CAE的平分线．
（1）如图1，求证：AM∥BC；
（2）如图2，若D是BC中点，DN平分∠ADC交AM于点N，DQ平分∠ADB交AM的反向延长线于Q，判断△QDN的形状并说明理由．
（3）如图3，在（2）的条件下，若∠BAC＝90°将∠QDN绕点D旋转一定角度，DN交边AC于F，DQ交边AB于H，当S△ABC＝14时，则四边形AHDF的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的盒子里装有颜色不同的黑、白两种球共60个，它们除颜色不同外，其余都相同，王颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中搅匀，经过大量重复上述摸球的过程，发现摸到白球的频率定于0.25．
（1）请估计摸到白球的概率将会接近________；
（2）计算盒子里白、黑两种颜色的球各有多少个？
（3）如果要使摸到白球的概率为
，需要往盒子里再放入多少个白球？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
