
【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
(1)求证:四边形ABCF是矩形;
(2)若ED=EC,求证:EA=EG.

 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,点
,点![]() 在射线
在射线![]() 上运动(
上运动(![]() 点与
点与![]() 三点不重合),设
三点不重合),设![]() ,
,![]() ,
,![]() .
.

(1)如果点![]() 在
在![]() 两点之间运动时,
两点之间运动时,![]() 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;
(2)如果点![]() 在
在![]() 两点之外运动时,
两点之外运动时,![]() 之间有何数量关系?(只需写出结论,不必说明理由)
之间有何数量关系?(只需写出结论,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF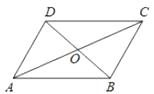
(1)根据题意,补全原形;
(2)求证:BE=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五月初,我市多地遭遇了持续强降雨的恶劣天气,造成部分地区出现严重洪涝灾害,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共2000件送往灾区,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同
(1)求甲、乙两种救灾物品每件的价格各是多少元?
(2)经调查,灾区对乙种物品件数的需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从友谊体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同、每个篮球的价格相同),若购买3个篮球和2个足球共需420元;购买2个篮球和4个足球共需440元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需要从该体育用品商店一次性购买足球和篮球共20个.要求购买篮球数不少于足球数的2倍,总费用不超过1840元,那么这所中学有哪几种购买方案?哪种方案所需费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com