
ЁОЬтФПЁПШчЭМЪЧБОЕиЧјвЛжжВњЦЗ30ЬьЕФЯњЪлЭМЯё,ЭМ1ЪЧВњЦЗЯњЪлСПy(Мў)гыЪБМфt(Ьь)ЕФКЏЪ§ЙиЯЕ,ЭМ2ЪЧвЛМўВњЦЗЕФЯњЪлРћШѓz(дЊ)гыЪБМфt(Ьь)ЕФКЏЪ§ЙиЯЕ,вбжЊШеЯњЪлРћШѓ=ШеЯњЪлСПЁСУПМўВњЦЗЕФЯњЪлРћШѓ,ЯТСаНсТлДэЮѓЕФЪЧЃЈ ЃЉЁЃ
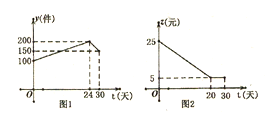
A. Ек24ЬьЕФЯњЪлСПЮЊ200МўB. Ек10ЬьЯњЪлвЛМўВњЦЗЕФРћШѓЪЧ15дЊ
C. Ек12ЬьгыЕк30ЬьетСНЬьЕФШеЯњЪлРћШѓЯрЕШD. Ек30ЬьЕФШеЯњЪлРћШѓЪЧ750дЊ
ЁОД№АИЁПC
ЁОНтЮіЁП
ЭМ1ЪЧВњЦЗШеЯњЪлСПyЃЈЕЅЮЛЃКМўЃЉгыЪБМфtЕЅЮЛЃКЬьЃЉЕФКЏЪ§ЭМЯѓЃЌЙлВьЭМЯѓПЩЖдAзіГіХаЖЯЃЛЭЈЙ§ЭМ2ЧѓГіzгыtЕФКЏЪ§ЙиЯЕЪНЃЌЧѓГіЕБt=10ЪБzЕФжЕЃЌзіГіЖдBЕФХаЖЯЃЌЗжБ№ЧѓГіЕк12ЬьКЭЕк30ЬьЕФЯњЪлРћШѓЃЌЖдCЁЂDНјааХаЖЯЃЎ
НтЃКAЁЂИљОнЭМЂйПЩЕУЕк24ЬьЕФЯњЪлСПЮЊ200МўЃЌЙЪе§ШЗЃЛ
BЁЂЩшЕБ0ЁмtЁм20ЃЌвЛМўВњЦЗЕФЯњЪлРћШѓzЃЈЕЅЮЛЃКдЊЃЉгыЪБМфtЃЈЕЅЮЛЃКЬьЃЉЕФКЏЪ§ЙиЯЕЮЊz=kx+bЃЌАбЃЈ0ЃЌ25ЃЉЃЌЃЈ20ЃЌ5ЃЉДњШыЕУЃК![]() ЃЌ
ЃЌ
ЕУЃЌz=-t+25ЃЈ0ЁмtЁм20ЃЉЃЌ
ЕБ20ЃМtЁм30ЪБКђЃЌгЩЭМ2жЊzЙЬЖЈЮЊ5ЃЌдђЃК
![]() ЃЌЃЌЕБt=10ЪБЃЌz=15ЃЌвђДЫBвВЪЧе§ШЗЕФЃЛ
ЃЌЃЌЕБt=10ЪБЃЌz=15ЃЌвђДЫBвВЪЧе§ШЗЕФЃЛ
CЁЂЕк12ЬьЕФЯњЪлРћШѓЮЊЃК[100+ЃЈ200-100ЃЉЁТ24ЁС12]ЃЈ25-12ЃЉ=2150дЊЃЌЕк30ЬьЕФЯњЪлРћШѓЮЊЃК150ЁС5=750дЊЃЌВЛЯрЕШЃЌЙЪCДэЮѓЃЛ
DЁЂЕк30ЬьЕФЯњЪлРћШѓЮЊЃК150ЁС5=750дЊЃЌе§ШЗЃЛ
ЙЪбЁЃКC.


 ПЊаФПьРжМйЦкзївЕЪюМйзївЕЮїАВГіАцЩчЯЕСаД№АИ
ПЊаФПьРжМйЦкзївЕЪюМйзївЕЮїАВГіАцЩчЯЕСаД№АИ УћЬтбЕСЗЯЕСаД№АИ
УћЬтбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЎ
ЃЈ1ЃЉгУдВЙцКЭжБГпдкACЩЯзїЕуPЃЌЪЙЕуPЕНAЁЂBЕФОрРыЯрЕШЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈКЭжЄУїЃЉ
ЃЈ2ЃЉЕБТњзуЃЈ1ЃЉЕФЕуPЕНABЁЂBCЕФОрРыЯрЕШЪБЃЌЧѓЁЯAЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
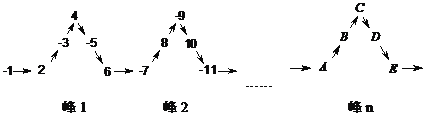
ЁОЬтФПЁПНЋвЛСагаРэЪ§-1ЃЌ2ЃЌ-3ЃЌ4ЃЌ-5ЃЌ6ЃЌЁЁЃЌШчЭМЫљЪОгаађХХСа.ИљОнЭМжаЕФХХСаЙцТЩПЩжЊЃЌЁАЗх1ЁБжаЗхЖЅЕФЮЛжУ(CЕФЮЛжУ)ЪЧгаРэЪ§4.дђ-2019гІХХдкAЃЌBЃЌCЃЌDЃЌEжа______ЕФЮЛжУ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮжНЦЌABCDжаЃЌAB=6ЃЌBC=8ЃЎАбЁїBCDбиЖдНЧЯпBDелЕўЃЌЪЙЕуCТфдкCЁфДІЃЌBCЁфНЛADгкЕуGЃЛEЁЂFЗжБ№ЪЧCЁфDКЭBDЩЯЕФЕуЃЌЯпЖЮEFНЛADгкЕуHЃЌАбЁїFDEбиEFелЕўЃЌЪЙЕуDТфдкDЁфДІЃЌЕуDЁфЧЁКУгыЕуAжиКЯЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїABGЁеЁїCЁфDGЃЛ
ЃЈ2ЃЉЧѓtanЁЯABGЕФжЕЃЛ
ЃЈ3ЃЉЧѓEFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБНЧЁїABCЕФШ§ИіЖЅЕуЗжБ№ЪЧAЃЈЉ3ЃЌ1ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌCЃЈ0ЃЌ1ЃЉ

ЃЈ1ЃЉНЋЁїABCвдЕуCЮЊа§зЊжааФа§зЊ180ЁуЃЌЛГіа§зЊКѓЖдгІЕФЁїA1B1C1ЃЛ
ЃЈ2ЃЉЗжБ№СЌНсAB1ЁЂBA1КѓЃЌЧѓЫФБпаЮAB1A1BЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЦНааЫФБпаЮABCDжа,вдЖЅЕуAЮЊдВаФ,ADГЄЮЊАыОЖ,дкABБпЩЯНиШЁAE=AD,гУГпЙцзїЭМЗЈзїГіЁЯBADЕФНЧЦНЗжЯпAG,ШєAD=5,DE=6,дђAGЕФГЄЪЧ_________________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
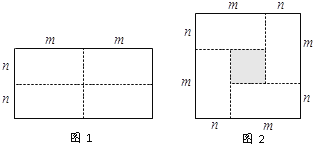
ЁОЬтФПЁПЭМ1ЪЧвЛИіГЄЮЊ2mЃЌПэЮЊ2nЕФГЄЗНаЮЃЌбиЭМжаащЯпгУМєЕЖОљЗжГЩЫФПщаЁГЄЗНаЮЃЌШЛКѓАДЭМ2ЕФЗНЗЈЦДГЩвЛИіБпГЄЮЊ(mЃЋn)ЕФе§ЗНаЮЃЎ
ЂХ ЧыгУСНжжВЛЭЌЕФЗНЗЈЧѓЭМ2жавѕгАВПЗжЕФУцЛ§ЃЎ
ЗНЗЈ1ЃК ЁЁ ЃЛЗНЗЈ2ЃК ЁЁ ЃЛ
ЂЦ ЙлВьЭМ2аДГі![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ИіДњЪ§ЪНжЎМфЕФЕШСПЙиЯЕЃК ЃЛ
Ш§ИіДњЪ§ЪНжЎМфЕФЕШСПЙиЯЕЃК ЃЛ
ЂЧ ИљОнЂЦжаФуЗЂЯжЕФЕШСПЙиЯЕЃЌНтОіШчЯТЮЪЬтЃКШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌетЪЧЭјЩЯЪЂДЋЕФвЛИіЙигкЪ§бЇЕФЙюБчЮЪЬтНиЭМЃЌБэ1ЪЧЫќЕФЪОвтБэ.ЮвУЧвЛЦ№РДНтД№ЁАЮЊЪВУДЖрГіСЫ2дЊ".

ЛЈШЅ | ЪЃгр | |
ТђХЃШт | 40дЊ | 60дЊ |
ТђжэНХ | 30дЊ | 30дЊ |
ТђЪпВЫ | 18дЊ | 12дЊ |
ТђЕїСЯ | 12дЊ | 0дЊ |
змМЦ | 100дЊ | 102дЊ |
Бэ1
ЛЈШЅ | ЪЃгр | |
ТђХЃШт | 40дЊ | 60дЊ |
ТђжэНХ | 30дЊ | 30дЊ |
ТђЪпВЫ | дЊ | дЊ |
ТђЕїСЯ | дЊ | 0дЊ |
змМЦ | 100дЊ | 103дЊ |
Бэ2
ЛЈШЅ | ЪЃгр | |
ТђЮяЦЗ1 | aдЊ | xдЊ |
ТђЮяЦЗ2 | bдЊ | yдЊ |
ТђЮяЦЗ3 | cдЊ | zдЊ |
ТђЮяЦЗ4 | dдЊ | 0дЊ |
змМЦ | 100дЊ | wдЊ |
Бэ3
ЛЈШЅ | ЪЃгр | |
ТђХЃШт | дЊ | дЊ |
ТђжэНХ | дЊ | дЊ |
ТђЪпВЫ | дЊ | дЊ |
ТђЕїСЯ | дЊ | дЊ |
змМЦ | дЊ | / |
Бэ4
(1)ЮЊСЫНтЪЭЁАЪЃгрН№ЖюзмМЦЁБгыЁАЮвЪжРяга100дЊ"ЮоЙиЃЌЧыАДвЊЧѓЬюаДБэ2жаЕФПеИё.
(2)ШчБэ3жаЃЌжБНгаДГіИїДњЪ§ЪНЕФжЕ: .
Ђйa+b+c+d=_ ЃЛ
Ђкa+x=__ ЃЛ
Ђлa+b+y=_ ЃЛ
Ђмa+b+c+z=_ ЁЃ
(3)ШчБэ3жаЃЌaЁЂbЁЂcЁЂdЖМЪЧе§ећЪ§ЃЌдђwЕФзюДѓжЕЕШгк_ ЃЌзюаЁжЕЕШгк_ ЃЌгЩДЫПЩвджЊЕРЁАЮЊЪВУДЖрГіСЫ2дЊЁБжЛЪЧвЛИіЙюБчЖјвб.
(4)ЮвУЧНЋЁАЛЈШЅЁБМЧЮЊЁАвЛЁБЃЌЁАЪЃгрЁБМЧЮЊЁА+ЁБЃЌЧыдкБэ4жаНЋБэ1Ъ§ОнжиаТЬюаД.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
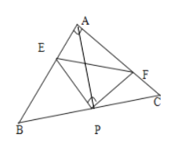
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌAB=ACЃЌЁЯBAC=90ЁуЃЌжБНЧШ§НЧаЮEPFЕФЖЅЕуPЪЧBCЕФжаЕуЃЌСНБпPEЁЂPFЗжБ№НЛABЁЂACгкЕуEЁЂFЃЌИјГівдЯТЮхИіНсТлЃКЂйAE=CFЃЛЂкЁЯAPE=ЁЯCPFЃЛЂлЁїEPFЪЧЕШбќжБНЧШ§НЧаЮЃЛЂмEF=APЃЛЂн![]() ЃЌЕБЁЯEPFдкЁїABCФкШЦЖЅЕуPа§зЊЪБЃЈЕуEВЛгыAЁЂBжиКЯЃЉЩЯЪіНсТле§ШЗЕФЪЧ_____________ЃЎЃЈЬюађКХЃЉ
ЃЌЕБЁЯEPFдкЁїABCФкШЦЖЅЕуPа§зЊЪБЃЈЕуEВЛгыAЁЂBжиКЯЃЉЩЯЪіНсТле§ШЗЕФЪЧ_____________ЃЎЃЈЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com