
【题目】如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.

(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
【答案】(1)根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论;
(2)由(1)可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,进而得出tan∠ABG的值;
(3)由△AEF是△DEF翻折而成可知EF垂直平分AD,故HD=![]() AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
试题解析:(1)∵△BDC′由△BDC翻折而成,
∴∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,
∴∠ABG=∠ADE,
在△ABG与△C′DG中,
∵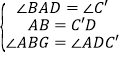 ,
,
∴△ABG≌△C′DG(AAS);
(2)∵由(1)可知△ABG≌△C′DG,
∴GD=GB,
∴AG+GB=AD,
设AG=x,则GB=8-x,
在Rt△ABG中,
∵AB2+AG2=BG2,
即62+x2=(8-x)2,
解得x=![]() ,
,
∴tan∠ABG=![]() ;
;
(3)∵△AEF是△DEF翻折而成,
∴EF垂直平分AD,
∴HD=![]() AD=4,
AD=4,
∴tan∠ABG=tan∠ADE=![]() ,
,
∴EH=HD×![]() =4×
=4×![]() =
=![]() ,
,
∵EF垂直平分AD,AB⊥AD,
∴HF是△ABD的中位线,
∴HF=![]() AB=
AB=![]() ×6=3,
×6=3,
∴EF=EH+HF=![]() +3=
+3=![]() .
.


科目:初中数学 来源: 题型:
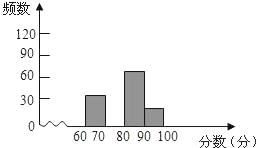
【题目】为迎接国庆60周年,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x<100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)表中m和n所表示的数分别为:m= ,n= ;
(2)请在图中,补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段;
(4)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
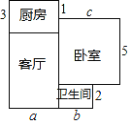
【题目】小王家新买的一套住房的建筑平面图如图所示(单位:米).
(1)这套住房的建筑总面积是多少平方米?(用含a,b,c的式子表示)
(2)若a=10,b=4,c=7,试求出小王家这套住房的具体面积.
(3)地面装修要铺设瓷砖,公司报价是:客厅地面每平方米240元,卧室地面每平方米220元,厨房地面每平方米180元,卫生间地面每平方米150元.在(2)的条件下,小王一共要花多少钱?
(4)这套住房的售价为每平方米15000元,购房时首付款为房价的40%,余款向银行申请贷款,在(2)的条件下,小王家购买这套住房时向银行申请贷款的金额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
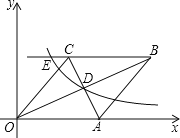
【题目】已知如图,四边形OABC为菱形,A点的坐标为![]() ,对角线OB、AC相交于D点,双曲线
,对角线OB、AC相交于D点,双曲线![]() 经过D点,交BC的延长线于E点,且
经过D点,交BC的延长线于E点,且![]() ,则E点的坐标是
,则E点的坐标是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图像,图1是产品销售量y(件)与时间t(天)的函数关系,图2是一件产品的销售利润z(元)与时间t(天)的函数关系,已知日销售利润=日销售量×每件产品的销售利润,下列结论错误的是( )。
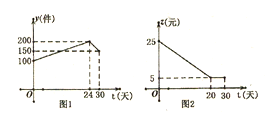
A. 第24天的销售量为200件B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:
(1)若从中抽出2张卡片,且这2个数字的差最小,应如何抽取?最小值是多少?
(2)若从中抽出2张卡片,且这2个数字的积最大,应如何抽取?最小值是多少?
(3)若从中抽出4张卡片,运用加、减、乘、除、乘方、括号等运算符号,使得结果为24.请写出运算式.(只需写出一种)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是平行四边形ABCD的边BC的中点,连接AE并延长交DC的延长线于点F,连接AC、BF,∠AEC=2∠ABC;(1)求证:四边形ABFC是矩形;(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com