
【题目】如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
(1)若OC恰好是∠AOE的平分线,则OA是∠COF的平分线吗?请说明理由;
(2)若∠EOF=5∠BOD,求∠COE的度数.
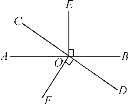
【答案】(1)OA是∠COF的平分线;(2)∠COE=60°
【解析】
(1)利用角平分线的性质和垂直的定义易得∠AOC=![]() ∠AOE=45°,再由OF⊥CD,可得∠COF=90°,易得∠AOF,由垂直的定义可得结论;
∠AOE=45°,再由OF⊥CD,可得∠COF=90°,易得∠AOF,由垂直的定义可得结论;
(2)设∠AOC=x,易得∠BOD=x,可得∠COE=90°-x,∠EOF=180°-x,利用∠EOF=5∠BOD,解得x,可得∠COE.
(1)OA是∠COF的平分线.
∵OE⊥AB,
∴∠AOE=90°,
∵OC恰好是∠AOE的平分线,
∴∠AOC=![]() ∠AOE=45°,
∠AOE=45°,
∵OF⊥CD,
∴∠COF=90°,
∴∠AOF=∠COF-∠AOC=90°-45°=45°,
∴OA是∠COF的平分线;
(2)设∠AOC=x,
∴∠BOD=x,
∵∠AOE=90°,
∴∠COE=∠AOE-∠AOC=90°-x,
∴∠EOF=∠COE+∠COF=90°-x+90°=180°-x,
∵∠EOF=5∠BOD,
∴180°-x=5x,
解得x=30,
∴∠COE=90°-30°=60°.


科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形 ABCD中,O为 AC 的中点,过点O的直线分别与AB,CD交于点E,F,连接 BF交AC于点M连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①△AOE≌△COF;②△EOB≌△CMB;③FB⊥OC,OM=CM;④四边形 EBFD 是菱形;⑤MB:OE=3:2其中正确结论的个数是( )
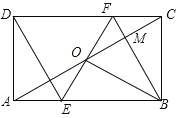
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九(1)、九(2)两班的班长交流了为四川安雅地震灾区捐款的情况:
(Ⅰ)九(1)班班长说:“我们班捐款总数为1200元,我们班人数比你们班多8人.”
(Ⅱ)九(2)班班长说:“我们班捐款总数也为1200元,我们班人均捐款比你们班人均捐款多20%.”
请根据两个班长的对话,求这两个班级每班的人均捐款数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
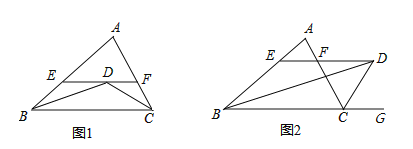
【题目】(1)如图1所示,在△ABC中,EF∥BC,点D在EF上,BD、CD分别平分∠ABC、∠ACB,若已知BE=3,CF=5,求EF的长度;
(2)如图2所示,BD平分∠ABC、CD平分∠ACG,DE∥BC交AB于点E,交AC于点F,线段EF与BE、CF有什么数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电脑中有一种游戏——蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下:①操作一次减x分;②每完成一列加y分.有一次小明在玩这种“蜘蛛纸牌”游戏时,随手用表格记录了两个时段的电脑显示:
第一时段 | 第二时段 | |
完成列数 | 2 | 5 |
分数 | 634 | 898 |
操作次数 | 66 | 102 |
(1)通过列方程组,求x,y的值;
(2)如果小明最终完成此游戏(即完成10列),分数是1 182,问他一共操作了多少次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边上的点F处,若AD=2,BC=6,则EF的值是( )
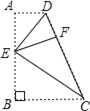
A. 2![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程 ![]() ,操作步骤是:
,操作步骤是:
第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C 的横坐标m即为该方程的一个实数根(如图1)
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D 的横坐标为n即为该方程的另一个实数根。

(1)在图2 中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹)
(2)结合图1,请证明“第三步”操作得到的m就是方程 ![]() 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程 ![]() 的实数根,请你直接写出一对固定点的坐标;
的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与a,b,c之间满足怎样的关系时,点P(
与a,b,c之间满足怎样的关系时,点P( ![]() ,
, ![]() ),Q(
),Q( ![]() ,
, ![]() )就是符合要求的一对固定点?
)就是符合要求的一对固定点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com