
【题目】如何求tan75°的值?按下列方法作图可解决问题.如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD.连接此图可求得tan75°的值为( )
A.2- ![]()
B.2+ ![]()
C.1+ ![]()
D.![]()
-1
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )

A. 2个 B. 3个 C. 4个 D. 无数个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产![]() 、
、![]() 两种产品共50件.已知生产一件
两种产品共50件.已知生产一件![]() 种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件
种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件![]() 种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
(1)设生产![]() 种产品
种产品![]() 件,完成表格:
件,完成表格:
|
| |
生产数量(件 |
| 件 |
需甲种原料(千克) |
|
|
需乙种原料(千克) |
|
|
(2)按要求安排![]() 、
、![]() 两种产品的件数有几种方案?请你设计出来.
两种产品的件数有几种方案?请你设计出来.
(3)以上方案哪种利润最大?是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热气球的探测器显示,从热气球A看一栋楼顶部B的仰角α为45°,看这栋楼底部C的俯角β为60°,热气球与楼的水平距离为100m,求这栋楼的高度(结果保留根号).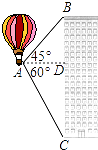
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.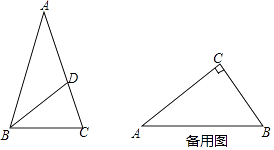
(1)等边三角形“內似线”的条数为;
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OM,ON分别是∠BOC和∠AOC的角平分线,∠AOB=86°,(1)∠MON=______(度);(2)当OC在∠AOB内绕点O转动时,∠MON的值______改变(填“会”或“不会”).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实行阶梯电价制度,居民家庭每月用电量不超过80千瓦时时,实行“基本电价”;当每月用电量超过80千瓦时时,超过部分实行“提高电价”.去年小张家4月用电量为100千瓦时,交电费68元;5月用电量为120千瓦时,交电费88元.则基本电价”是__元/千瓦时,“提高电价”是__元/千瓦时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com