
【题目】![]() ,
,![]() 两地相距
两地相距![]() .甲、乙两人都由
.甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]() .
.
(1)根据题意,填写下表:
时间 与 | 0.5 | 1.8 | ______ |
甲与 | 5 | ______ | 20 |
乙与 | 0 | 12 | ______ |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() ,写出
,写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】学校准备购置一批教师办公桌椅,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求一套A型桌椅和一套B型桌椅的售价各是多少元;
(2)学校准备购进这两种型号的办公桌椅200套,平均每套桌椅需要运费10元,并且A型桌椅的套数不多于B型桌椅的套数的3倍.请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
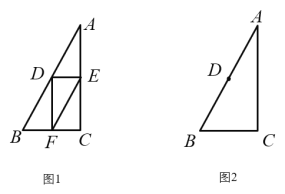
【题目】在![]() 中,∠C=90°,AC>BC,D是AB的中点.E为直线上一动点,连接DE,过点D作DF⊥DE,交直线BC于点F,连接EF.
中,∠C=90°,AC>BC,D是AB的中点.E为直线上一动点,连接DE,过点D作DF⊥DE,交直线BC于点F,连接EF.
(1)如图1,当E是线段AC的中点时,设![]() ,求EF的长(用含
,求EF的长(用含![]() 的式子表示);
的式子表示);
(2)当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE,EF,BF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在⊙O中,弦AB与CD相交于点F,∠BCD=68°,∠CFA=108°,求∠ADC的度数.
(2)如图2,在正方形ABCD中,点E是CD上一点(DE>CE),连接AE,并过点E作AE的垂线交BC于点F,若AB=9,BF=7,求DE长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】例 如图①,李老师设计了一个探究杠杆平衡条件的实验:在一个自制的类似天平的仪器的左边固定托盘![]() 中放置一个重物,在右边活动托盘
中放置一个重物,在右边活动托盘![]() (可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘
(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘![]() 与点
与点![]() 的距离
的距离![]() ,观察活动托盘
,观察活动托盘![]() 中砝码的质量
中砝码的质量![]() 的变化情况.实验数据记录如表:
的变化情况.实验数据记录如表:
| 10 | 15 | 20 | 25 | 30 |
| 30 | 20 | 15 | 12 | 10 |
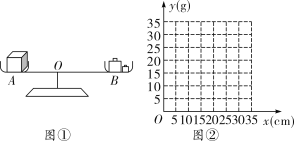
(1)把表中![]() 的各组对应值作为点的坐标,在图②的坐标系中描出相应的点,用平滑曲线连接这些点;
的各组对应值作为点的坐标,在图②的坐标系中描出相应的点,用平滑曲线连接这些点;
(2)观察所画的图象,猜测![]() 与
与![]() 之间的函数关系,求出函数关系式;
之间的函数关系,求出函数关系式;
(3)当砝码的质量为![]() 时,活动托盘
时,活动托盘![]() 与点
与点![]() 的距离是多少?
的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种植基地种植一种蔬菜,它的成本是每千克2元,售价是每千克3元,年销量为10万千克.基地准备拿出一定的资金作绿色开发,若每年绿色开发投入的资金为![]() (万元),该种蔬菜的年销量将是原年销量的
(万元),该种蔬菜的年销量将是原年销量的![]() 倍,
倍,![]() 与
与![]() 的关系如下表:
的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 1 | 1.5 | 1.8 | 1.9 | 1.8 | 1.5 | … |
(1)猜想![]() 与
与![]() 之间的函数类型是________函数,求出该函数的表达式并验证;
之间的函数类型是________函数,求出该函数的表达式并验证;
(2)求年利润![]() (万元)与绿色开发投入的资金
(万元)与绿色开发投入的资金![]() (万元)之间的函数关系式,当绿色开发投入的资金不低于3万元,又不超过5万元时,求此时年利润
(万元)之间的函数关系式,当绿色开发投入的资金不低于3万元,又不超过5万元时,求此时年利润![]() (万元)的最大值;
(万元)的最大值;
(注:年利润![]() 销售总额-成本费-绿色开发投入的资金)
销售总额-成本费-绿色开发投入的资金)
(3)若提高种植人员的奖金,发现又增加一部分年销量,经调查发现:再次增加的年销量![]() (万千克)与每年提高种植人员的奖金
(万千克)与每年提高种植人员的奖金![]() (万元)之间满足
(万元)之间满足![]() ,若基地将投入5万元用于绿色开发和提高种植人员的奖金,应怎样分配这笔资金才能使总年利润达到17万元且绿色开发投入大于奖金投入?(
,若基地将投入5万元用于绿色开发和提高种植人员的奖金,应怎样分配这笔资金才能使总年利润达到17万元且绿色开发投入大于奖金投入?(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于
的图象相交于![]() ,
,![]() 两点.
两点.
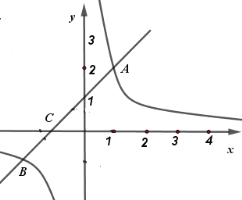
(1)求一次函数和反比例函数的表达式;
(2)直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 轴上的点,若
轴上的点,若![]() 的面积是
的面积是![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com