
【题目】在![]() 中,射线
中,射线![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 边上运动(不与点
边上运动(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
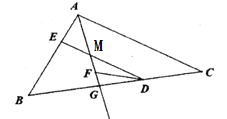
(1)如图1,点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 平分
平分![]() .
.


①若![]() ,
,![]() ,则
,则![]() _____;若
_____;若![]() ,则
,则![]() _____;
_____;
②试探究![]() 与
与![]() 之间的数量关系?请说明理由;
之间的数量关系?请说明理由;
(2)点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 的角平分线所在直线与射线
的角平分线所在直线与射线![]() 交于点
交于点![]() .试探究
.试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)①115°,110°;②![]() ,证明见解析;(2)
,证明见解析;(2)![]() ,证明见解析.
,证明见解析.
【解析】
(1)①根据角平分线的定义求得∠CAG=![]() ∠BAC=50°;再由平行线的性质可得∠EDG=∠C=30°,∠FMD=∠GAC=50°;由三角形的内角和定理求得∠AFD的度数即可;已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=
∠BAC=50°;再由平行线的性质可得∠EDG=∠C=30°,∠FMD=∠GAC=50°;由三角形的内角和定理求得∠AFD的度数即可;已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=![]() ∠BAC,∠FDM=
∠BAC,∠FDM=![]() ∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;即可得∠FDM +∠FMD=
∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;即可得∠FDM +∠FMD=![]() ∠EDG +∠GAC=
∠EDG +∠GAC=![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×140°=70°;再由三角形的内角和定理可求得∠AFD=110°;②∠AFD=90°+
×140°=70°;再由三角形的内角和定理可求得∠AFD=110°;②∠AFD=90°+![]() ∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=
∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=![]() ∠BAC,∠FDM=
∠BAC,∠FDM=![]() ∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;由此可得∠FDM +∠FMD=
∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;由此可得∠FDM +∠FMD=![]() ∠EDG +∠GAC=
∠EDG +∠GAC=![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×(180°-∠B)=90°-
×(180°-∠B)=90°-![]() ∠B;再由三角形的内角和定理可得∠AFD=90°+
∠B;再由三角形的内角和定理可得∠AFD=90°+![]() ∠B;(2)∠AFD=90°-
∠B;(2)∠AFD=90°-![]() ∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=
∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=![]() ∠BAC,∠NDE=
∠BAC,∠NDE=![]() ∠EDB,即可得∠FDM=∠NDE=
∠EDB,即可得∠FDM=∠NDE=![]() ∠EDB;由DE//AC,根据平行线的性质可得∠EDB=∠C,∠FMD=∠GAC;即可得到∠FDM=∠NDE=
∠EDB;由DE//AC,根据平行线的性质可得∠EDB=∠C,∠FMD=∠GAC;即可得到∠FDM=∠NDE=![]() ∠C,所以∠FDM +∠FMD =
∠C,所以∠FDM +∠FMD =![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×(180°-∠B)=90°-
×(180°-∠B)=90°-![]() ∠B;再由三角形外角的性质可得∠AFD=∠FDM +∠FMD=90°-
∠B;再由三角形外角的性质可得∠AFD=∠FDM +∠FMD=90°-![]() ∠B.
∠B.
(1)①∵AG平分∠BAC,∠BAC=100°,
∴∠CAG=![]() ∠BAC=50°;
∠BAC=50°;
∵![]() ,∠C=30°,
,∠C=30°,
∴∠EDG=∠C=30°,∠FMD=∠GAC=50°;
∵DF平分∠EDB,
∴∠FDM=![]() ∠EDG=15°;
∠EDG=15°;
∴∠AFD=180°-∠FMD-∠FDM=180°-50°-15°=115°;
∵∠B=40°,
∴∠BAC+∠C=180°-∠B=140°;
∵AG平分∠BAC,DF平分∠EDB,
∴∠CAG=![]() ∠BAC,∠FDM=
∠BAC,∠FDM=![]() ∠EDG,
∠EDG,
∵DE//AC,
∴∠EDG=∠C,∠FMD=∠GAC;
∴∠FDM +∠FMD=![]() ∠EDG +∠GAC=
∠EDG +∠GAC=![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×140°=70°;
×140°=70°;
∴∠AFD=180°-(∠FDM +∠FMD)=180°-70°=110°;
故答案为:115°,110°;
②∠AFD=90°+![]() ∠B,理由如下:
∠B,理由如下:
∵AG平分∠BAC,DF平分∠EDB,
∴∠CAG=![]() ∠BAC,∠FDM=
∠BAC,∠FDM=![]() ∠EDG,
∠EDG,
∵DE//AC,
∴∠EDG=∠C,∠FMD=∠GAC;
∴∠FDM +∠FMD=![]() ∠EDG +∠GAC=
∠EDG +∠GAC=![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×(180°-∠B)=90°-
×(180°-∠B)=90°-![]() ∠B;
∠B;
∴∠AFD=180°-(∠FDM +∠FMD)=180°-(90°-![]() ∠B)=90°+
∠B)=90°+![]() ∠B;
∠B;
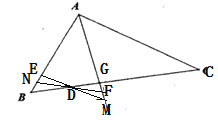
(2)∠AFD=90°-![]() ∠B,理由如下:
∠B,理由如下:
如图,射线ED交AG于点M,
∵AG平分∠BAC,DF平分∠EDB,
∴∠CAG=![]() ∠BAC,∠NDE=
∠BAC,∠NDE=![]() ∠EDB,
∠EDB,
∴∠FDM=∠NDE=![]() ∠EDB,
∠EDB,
∵DE//AC,
∴∠EDB=∠C,∠FMD=∠GAC;
∴∠FDM=∠NDE=![]() ∠C,
∠C,
∴∠FDM +∠FMD =![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×(180°-∠B)=90°-
×(180°-∠B)=90°-![]() ∠B;
∠B;
∴∠AFD=∠FDM +∠FMD=90°-![]() ∠B.
∠B.


科目:初中数学 来源: 题型:
【题目】阅读下题和解题过程:化简![]() ,使结果不含绝对值.
,使结果不含绝对值.
解:当![]() 时,即
时,即![]() 时,
时,
原式![]()
![]() ;
;
当![]() ,即
,即![]() 时,
时,
原式![]()
![]()
这种解题的方法叫“分类讨论法”.
(1)请你用“分类讨论法”解一元一次方程:![]() ;
;
(2)试探究:当![]() 分别为何值时,方程
分别为何值时,方程![]()
①无解,②只有一个解,③有两个解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
请你根据上述解题思路解答下面问题:
(1)已知a﹣b=﹣3,ab=﹣2,求(a+b)(a2﹣b2)的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8, ![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,把
,把![]() 的直角三角板
的直角三角板![]() 的直角顶点
的直角顶点![]() 放在直线
放在直线![]() 上.将直角三角板
上.将直角三角板![]() 在平面内绕点
在平面内绕点![]() 任意转动,若转动的过程中,直线
任意转动,若转动的过程中,直线![]() 与直线
与直线![]() 的夹角为60°,则
的夹角为60°,则![]() 的度数为___.
的度数为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(结果精确到0.1m。参考数据:tan20°≈0.36,tan18°≈0.32)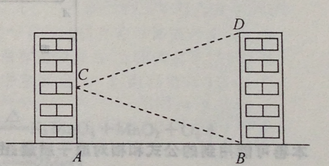
(1)求∠BCD的度数.
(2)求教学楼的高BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)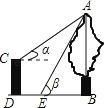
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求: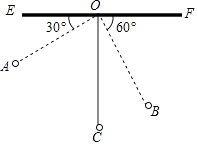
(1)单摆的长度( ![]() ≈1.7);
≈1.7);
(2)从点A摆动到点B经过的路径长(π≈3.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
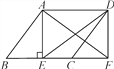
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com