
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE. 
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.
【答案】
(1)解:如图所示:
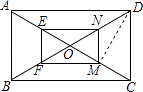
(2)证明:∵点E,F分别为OA,OB的中点,
∴EF∥AB,EF= ![]() AB,
AB,
同理:NM∥CD,MN= ![]() DC,
DC,
∵四边形ABCD是矩形,
∴AB∥DC,AB=DC,AC=BD,
∴EF∥NM,EF=MN,
∴四边形EFMN是平行四边形,
∵点E,F,M,N分别为OA,OB,OC,OD的中点,
∴EO= ![]() AO,MO=
AO,MO= ![]() CO,
CO,
在矩形ABCD中,AO=CO= ![]() AC,BO=DO=
AC,BO=DO= ![]() BD,
BD,
∴EM=EO+MO= ![]() AC,
AC,
同理可证FN= ![]() BD,
BD,
∴EM=FN,
∴四边形EFMN是矩形
(3)解:∵DM⊥AC于点M,
由(2)MO= ![]() CO,
CO,
∴DO=CD,
在矩形ABCD中,
AO=CO= ![]() AC,BO=DO=
AC,BO=DO= ![]() BD,AC=BD,
BD,AC=BD,
∴AO=BO=CO=DO,
∴△COD是等边三角形,
∴∠ODC=60°,
∵MN∥DC,
∴∠FNM=∠ODC=60°,
在矩形EFMN中,∠FMN=90°.
∴∠NFM=90°﹣∠FNM=30°,
∵NO=3,
∴FN=2NO=6,FM=3 ![]() ,MN=3,
,MN=3,
∵点F,M分别为OB,OC的中点,
∴BC=2FM=6 ![]() ,
,
∴矩形的面积为BCCD=36 ![]()
【解析】(1)根据题目要求画出图形即可;(2)根据三角形中位线定理可得EF∥AB,EF= ![]() AB,NM∥CD,MN=
AB,NM∥CD,MN= ![]() DC,再由矩形的性质可得AB∥DC,AB=DC,AC=BD,进而可得四边形EFMN是矩形;(3)根据条件可得DM垂直平分OC,进而可得DO=CO,然后证明△COD是等边三角形,进而得出BC,CD的长,进而得出答案.
DC,再由矩形的性质可得AB∥DC,AB=DC,AC=BD,进而可得四边形EFMN是矩形;(3)根据条件可得DM垂直平分OC,进而可得DO=CO,然后证明△COD是等边三角形,进而得出BC,CD的长,进而得出答案.


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为![]() ,
,![]() ,
,![]() ,各边上的内接正方形的边长分别记为
,各边上的内接正方形的边长分别记为![]() ,
,![]() ,
,![]() .
.
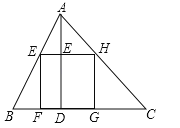
(1)模拟探究:如图,正方形EFGH为△ABC的BC边上的内接正方形,求证:![]() ;
;
(2)特殊应用:若∠BAC=90°,![]() =
=![]() =2,求
=2,求![]() 的值;
的值;
(3)拓展延伸:若△ABC为锐角三角形,b<c,请判断![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年,中央财政安排资金 8 200 000 000 元,免除城市义务教育学生学杂费,支持进城务工人员随迁子女公平接受义务教育,这个数据用科学记数法可表示为元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A= ![]() ∠B=
∠B= ![]() ∠C
∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=2∠B=3∠C
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com