
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④ ![]() 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:∵b>a>0
∴﹣ ![]() <0,
<0,
所以①正确;
∵抛物线与x轴最多有一个交点,
∴b2﹣4ac≤0,
∴关于x的方程ax2+bx+c+2=0中,△=b2﹣4a(c+2)=b2﹣4ac﹣8a<0,
所以②正确;
∵a>0及抛物线与x轴最多有一个交点,
∴x取任何值时,y≥0
∴当x=﹣1时,a﹣b+c≥0;
所以③正确;
当x=﹣2时,4a﹣2b+c≥0
a+b+c≥3b﹣3a
a+b+c≥3(b﹣a)![]() ≥3
≥3
所以④正确.
故选:D.
从抛物线与x轴最多一个交点及b>a>0,可以推断抛物线最小值最小为0,对称轴在y轴左侧,并得到b2﹣4ac≤0,从而得到①②为正确;由x=﹣1及x=﹣2时y都大于或等于零可以得到③④正确.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
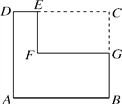
【题目】如图,四边形ABCD是边长为4的正方形,在正方形的一个角上剪去长方形CEFG,其中E,G分别是边CD,BC上的点,且CE=3,CG=2,剩余部分是六边形ABGFED,请你建立适当的直角坐标系求六边形ABGFED各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空完成推理过程:
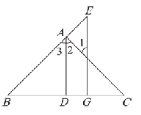
如图,AD⊥BC于点D,EG⊥BC于点G,AD平分∠BA C. 求证: ∠E=∠1.
证明: ∵AD⊥BC于点D,EG⊥BC于点G,(已知)
∴∠ADC=∠EGC=90°,(垂直的定义)
∴AD∥EG,( )
∴∠1= ,( )
∠E=∠3,(两直线平行,同位角相等)
∵AD平分∠BAC,(已知)
∴∠2=∠3,( )
∴∠E=∠1.(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4 cm,AD=12 cm,点P在AD边上以每秒1 cm的速度从点A向点D运动,点Q在BC边上,以每秒4 cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,当运动时间=_____时线段PQ∥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是( )
A. 7-2×(-![]() )=5×(-
)=5×(-![]() )=-1 B. -3÷7×
)=-1 B. -3÷7×![]() =-3÷1=-3
=-3÷1=-3
C. -32-(-3)2=-9-9=-18 D. 3×23-2×9=3×6-18=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD的平分线与∠ADC的平分线相交于点E,∠ABC的平分线与∠BCD的平分线相交于点F,则∠E与∠F的数量关系是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种商品的标准价格是200元,但随着季节的变化,商品的价格可浮动![]() ,想一想.
,想一想.
![]() 的含义是什么?
的含义是什么?
![]() 请你计算出该商品的最高价格和最低价格;
请你计算出该商品的最高价格和最低价格;
![]() 如果以标准价为标准,超过标准价记“
如果以标准价为标准,超过标准价记“![]() ”,低于标准价记“
”,低于标准价记“![]() ”,该商品价格的浮动范围又可以怎样表示?
”,该商品价格的浮动范围又可以怎样表示?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com