已知抛物线C1:y=x2-(2m+4)x+m2-10的顶点A到y轴的距离为3,与x轴交于C、D两点.
(1)求顶点A的坐标;(2)求C、D两点的坐标.
分析:(1)把抛物线一般表达式写成顶点式,知道顶点A到y轴的距离,进而求出m的值,写出抛物线顶点式表达式,求出坐标.
(2)由抛物线C1的解析式为y=x2-6x-9可知,与x轴有交点时,y=0,可得方程x2-6x-9=0,即可解得C、D两点坐标.
解答:解:(1)y=x
2-(2m+4)x+m
2-10
=[x-(m+2)]
2+m
2-10-(m+2)
2=[x-(m+2)]
2-4m-14,
∴抛物线顶点A的坐标为(m+2,-4m-14),
由于顶点A到y轴的距离为3,
∴|m+2|=3,
∴m=1或m=-5.
∵抛物线与x轴交于C、D两点,
∴m=-5时,△<0,则抛物线与x轴无交点,不符合题意,舍去.
∴m=1,
∴抛物线顶点A的坐标为(3,-18).
(2)解方程x
2-6x-9=0,得:
x1=3+3,x2=3-3∴C、D两点坐标分别为(
3+3,0)和(
3-3,0).
点评:本题是二次函数的综合应用题,考查抛物线的顶点坐标公式,会求解抛物线上的点的坐标.此题不是很难,但做题时也要小心仔细.



 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案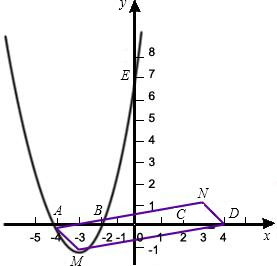 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).