练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，D为BC上一点，∠BAD=∠ABC，∠ADC=∠ACD，若∠BAC=63°，试求∠DAC、∠ADC的度数．

    【答案】∠DAC=24°，∠ADC=78°．

    【解析】

    试题设∠BAD=x°，根据∠BAD=∠ABC得到∠ADC=2∠BAD，从而得到∠ACD=2∠BAD，根据三角形内角和定理列出方程求出x的值，从而得到答案.

    试题解析：设∠BAD=．因为∠BAD=∠ABC，所以∠ADC=2∠BAD．又因为∠ADC=∠ACD，所以∠ACD=2∠BAD．因为∠BAC=63°，所以+∠DAC=63°，4+∠DAC=180°，所以∠DAC=24°，°，∠ADC=2×39°=78°．所以∠DAC=24°，∠ADC=78°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

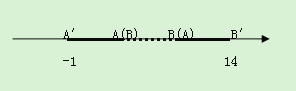
    【题目】(1)如图，在数轴上有一小木棒AB，若平移木棒，使B落在A处，则A′所表示的数为 -1，若将A落在B处时，则B′所表示的数14，它的两个端点A、B所表示的数分别是 、 .

    (2)老师给东东出了一道关于年龄的数学题：我像你那么小时，你才两岁；你像我那么大时，我已经44岁了，你猜我有多少岁？亲爱的同学，你能不能利用上一题的方法帮助小东求出老师的年龄呢？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

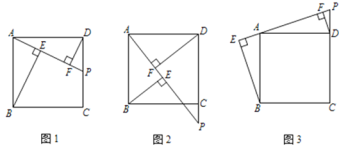
    【题目】在正方形中，，，是边上一点，连接，过点，作，，垂足分别为，，如图1．

    （1）请探究，，这三条线段有怎样的数量关系？请说明理由；

    （2）若点在的延长线上，如图2，那么这三条线段的数量关系是 （直接写结果）

    （3）若点在的延长线上，如图3，那么这三条线段的数量关系是 （直接写结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）若x，y都是实数，且，求5x+13y+6的立方根；

    （2）已知△ABC的三边长分别为a，b，c，且满足，求c的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现在正是草莓热销的季节，某水果零售商店分两批次从批发市场共购进草莓40箱，已知第一、二次进货价分别为每箱50元、40元，且第二次比第一次多付款700元．
    （1）设第一、二次购进草莓的箱数分别为a箱、b箱，求a，b的值；
    （2）若商店对这40箱草莓先按每箱60元销售了x箱，其余的按每箱35元全部售完． ①求商店销售完全部草莓所获利润y（元）与x（箱）之间的函数关系式；
    ②当x的值至少为多少时，商店才不会亏本．
    （注：按整箱出售，利润=销售总收入﹣进货总成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（ ）
    A.（ ）﹣2=9
    B. =﹣2
    C.（﹣2）0=﹣1
    D.|﹣5﹣3|=2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，数轴的单位长度为1．

    （1）如果点B，D表示的数互为相反数，那么图中点A、点D表示的数分别是 、 ；

    （2）当点B为原点时，在数轴上是否存在点M，使得点M到点A的距离是点M到点D的距离的2倍，若存在，请求出此时点M所表示的数；若不存在，说明理由；

    （3） 在（2）的条件下，点A、点C分别以2个单位长度/秒和0.5个单位长度同时向右运动，同时点P从原点出发以3个单位长度/秒的速度向左运动，当点A与点C之间的距离为3个单位长度时，求点P所对应的数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，我们把对角线互相垂直的四边形叫做垂美四边形．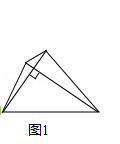

    （1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．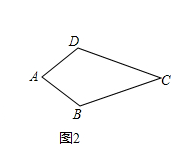

    （2）性质探究：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．
    猜想结论：（要求用文字语言叙述）
    写出证明过程（先画出图形，写出已知、求证）．
    （3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5，求GE长．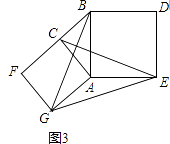

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知E、F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M，O为BD的中点，则下列结论：①∠AME=90°；②∠BAF=∠EDB；③∠BMO=90°；④MD=2AM=4EM；⑤AM= MF．其中正确结论的个数是（ ）
    A.5个
    B.4个
    C.3个
    D.2个

    查看答案和解析>>

    同步练习册答案