
����Ŀ����ͼ1�����ǰѶԽ����ഹֱ���ı��ν��������ı��Σ�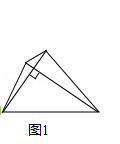
��1���������⣺��ͼ2�����ı���ABCD�У�AB=AD��CB=CD�����ı���ABCD�Ǵ����ı�������˵�����ɣ�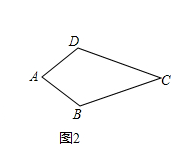
��2������̽������̽�������ı���ABCD����Ա�AB��CD��BC��AD֮���������ϵ��
������ۣ���Ҫ������������������ ![]()
д��֤�����̣��Ȼ���ͼ�Σ�д����֪����֤����
��3������������ͼ3���ֱ���Rt��ACB��ֱ�DZ�AC��б��ABΪ��������������ACFG��������ABDE������CE��BG��GE����֪AC=4��AB=5����GE����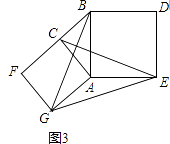
���𰸡�
��1��
�⣺�ı���ABCD�Ǵ����ı��Σ�
֤������AB=AD��
���A���߶�BD�Ĵ�ֱƽ�����ϣ�
��CB=CD��
���C���߶�BD�Ĵ�ֱƽ�����ϣ�
��ֱ��AC���߶�BD�Ĵ�ֱƽ���ߣ�
��AC��BD�����ı���ABCD�Ǵ����ı���
��2��
�⣺������ۣ������ı��ε�����Աߵ�ƽ������ȣ�
��ͼ2����֪�ı���ABCD�У�AC��BD������ΪE��
��֤��AD2+BC2=AB2+CD2
֤������AC��BD��
���AED=��AEB=��BEC=��CED=90�㣬
�ɹ��ɶ����ã�AD2+BC2=AE2+DE2+BE2+CE2��
AB2+CD2=AE2+BE2+CE2+DE2��
��AD2+BC2=AB2+CD2
��3��
�⣺����CG��BE��
�ߡ�CAG=��BAE=90�㣬
���CAG+��BAC=��BAE+��BAC������GAB=��CAE��
�ڡ�GAB�͡�CAE�У�
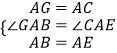 ��
��
���GAB�ա�CAE��
���ABG=��AEC���֡�AEC+��AME=90�㣬
���ABG+��AME=90�㣬��CE��BG��
���ı���CGEB�Ǵ����ı��Σ�
�ɣ�2���ã�CG2+BE2=CB2+GE2��
��AC=4��AB=5��
��BC=3��CG=4 ![]() ��BE=5
��BE=5 ![]() ��
��
��GE2=CG2+BE2��CB2=73��
��GE= ![]()

����������1�����ݴ�ֱƽ���ߵ��ж�����֤�����ɣ���2�����ݴ�ֱ�Ķ�����ɶ�����ɣ���3�����ݴ����ı��ε����ʡ����ɶ�������ϣ�2���Ľ��ۼ��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ߵij���3��4�������ߵij��Ƿ��� ![]() -12x+35=0�ĸ�����������ε��ܳ�Ϊ��������
-12x+35=0�ĸ�����������ε��ܳ�Ϊ��������
A.14
B.12
C.12��14
D.���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�DΪBC��һ�㣬��BAD=��ABC����ADC=��ACD������BAC=63����������DAC����ADC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��A=40�㣬��ABC����ǡ�CBD��ƽ����BE��AC���ӳ����ڵ�E��
��1�����CBE�Ķ�����
��2������D��DF��BE����AC���ӳ����ڵ�F�����F�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
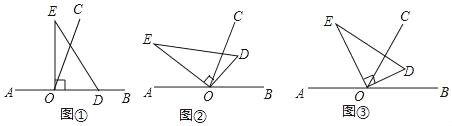
����Ŀ����ͼ����ֱ��AB��һ��OΪ�˵�������OC��ʹ��BOC=70������һ��ֱ�������ε�ֱ�Ƕ�����ڵ�O������ע����DOE=90�㣩
��1����ͼ�٣���ֱ�����ǰ�DOE��һ��OD��������OB�ϣ����COE=�� ���㣻
��2����ͼ�ڣ���ֱ�����ǰ�DOE�Ƶ�O��ʱ�뷽��ת����ij��λ�ã���OCǡ��ƽ�֡�BOE�����COD�Ķ�����
��3����ͼ�ۣ���ֱ�����ǰ�DOE�Ƶ�Oת�������ODʼ���ڡ�BOC���ڲ����Բ����BOD�͡�COE��������������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.һ����Ϸ���н������� ![]() ������10����������Ϸһ�����н�
������10����������Ϸһ�����н�
B.һ������6��8��7��8��8��9��10����������λ������8
C.Ϊ�˽�ȫ����ѧ�����������������Ӧ�ò����ղ�ķ�ʽ
D.���������ݵķ���S2��=0.01���������ݵķ���S2��=0.1�����������ݱȼ��������ȶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣
��1�����㣺��22+| ![]() ��4|+��
��4|+�� ![]() ����1+2tan60�㣮
����1+2tan60�㣮
��2���Ȼ�������ֵ���� ![]() ��
�� ![]() ����
���� ![]() ������x�Dz���ʽ3x+7��1�ĸ������⣮
������x�Dz���ʽ3x+7��1�ĸ������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������x�ύ��A����1��0����B��5��0�����㣬��y�ύ�ڵ�C��0��5����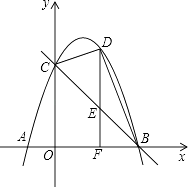
��1���������������Ӧ�ĺ�����ϵʽ��
��2��D����һ�������������ϵ�һ�����㣨���C��B���غϣ�������D��DF��x���ڵ�F����ֱ��BC�ڵ�E������BD��CD�����D�ĺ�����Ϊm����BCD�����ΪS��
����S����m�ĺ�����ϵʽ���Ա���m��ȡֵ��Χ��
�ڵ�mΪ��ֵʱ��S�����ֵ������������ֵ��
��ֱ��BC�ܷ�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣����ܣ��������D�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A��B��C�����㣬���DZ�ʾ�����ֱ���![]() ��
��![]() ��
��![]() ��
��

��1����գ�AB�� ��BC�� ��
��2�����ж���M��N����A���������M��ÿ��2����λ���ȵ��ٶ������ƶ�������M�ƶ���B��ʱ����N�Ŵ�A�����������ÿ��3����λ���ȵ��ٶ������ƶ������N�ƶ�����ʱ�䣬��N�ϵ�M��
��3������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��3����λ���Ⱥ�7����λ���ȵ��ٶ������˶�����̽����BC��AB��ֵ�Ƿ�����ʱ��ı仯���ı䣿��˵�����ɡ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com